
Problemas McGuffin
El concepto de MacGuffin cinematográfico, introducido por Alfred Hitchcock, es aplicable a algunos problemas de lógica y matemáticas

El concepto de MacGuffin cinematográfico, introducido por Alfred Hitchcock, es aplicable a algunos problemas de lógica y matemáticas

El matemático francés Eugène Ehrhart generalizó los trabajos de Pick y Reeve a los politopos de n dimensiones

El tetraedro de Reeve y la serpiente de Winkler: dos sencillos objetos matemáticos de interesantes implicaciones
El teorema de Pick permite hallar mediante una fórmula muy sencilla el área de un polígono encajado en una retícula

El ‘ostomachion’ o caja de Arquímedes es un rompecabezas milenario con claras similitudes con el tangram

¿Puede haber en el ajedrez una estrategia que garantice la victoria de las negras?
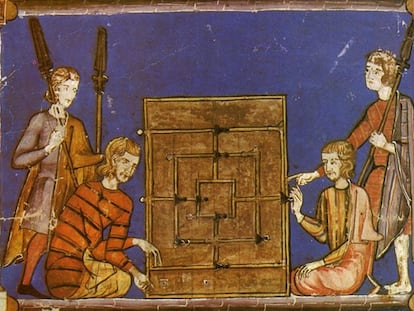
El molino (también conocido como Morris o Nueve hombres de Morris) es uno de los más populares juegos de tablero derivados del alquerque

El alquerque es un milenario juego de tablero que dio lugar a numerosas variantes, como el molino o las damas

En una partida de cartas el cálculo de probabilidades puede marcar la diferencia entre ganar y perder

El pájaro dodo de ‘Alicia en el País de las Maravillas’ representa al propio Carroll, que tartamudeaba al decir su apellido: Do… Do… Dodgson

El ortoédrico ladrillo une a su interés como cuerpo geométrico sus múltiples aplicaciones como objeto material

Los contenedores ortoédricos, como las cajas de cartón y los tetrabriks, dan lugar a interesantes problemas de optimización
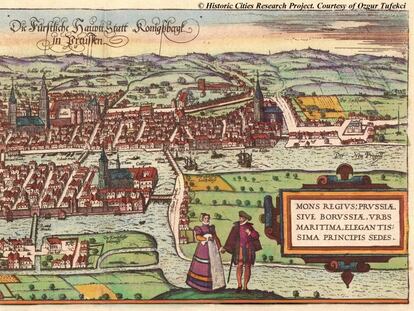
Euler introdujo la teoría de grafos al analizar el famoso problema de los puentes de Königsberg

La naturaleza, la historia y el lenguaje mismo ofrecen numerosos ejemplos de secuencias no numéricas

Los torneos y otras competiciones eliminatorias plantean problemas combinatorios no siempre fáciles de resolver

La voracidad es también un concepto informático y una forma de optimizar resultados

Los renos del trineo de Papá Noel y sus itinerarios se prestan a interesantes consideraciones combinatorias

Los dominós y trominós plantean interesantes problemas de teselación del tablero de ajedrez y otras superficies acotadas

Solomon W. Golomb y Martin Gardner estudiaron los mosaicos de poliominós sin líneas de fractura

Las particiones de los números naturales en sumandos fueron estudiadas por Hardy y Ramanujan a principios del siglo pasado
Las particiones de números naturales en sumandos constituyen un importante capítulo de las matemáticas discretas

No siempre es fácil repartir de forma equitativa y a gusto de todos, o tan siquiera saber cuántas partes se pueden obtener
Hay problemas que parecen imposibles de resolver, como algunos de los que aparecen en los libros de Clifford Pickover, y sin embargo…
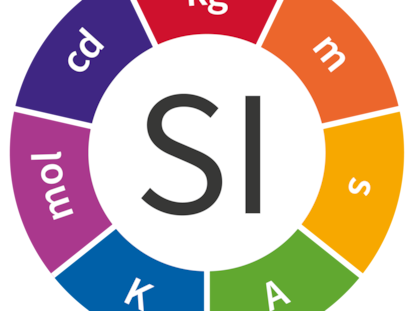
El Sistema Internacional define siete unidades básicas correspondientes a otras tantas magnitudes físicas fundamentales
No hay que confundir la masa con el peso ni con la cantidad de sustancia de un objeto físico

El matemático inglés Henry Briggs propuso los logaritmos decimales como alternativa a los neperianos

Además de inventar los logaritmos, John Napier ideó un ingenioso ábaco para simplificar las operaciones aritméticas

El agua no solo es el disolvente universal, sino también un referente para los sistemas de unidades

¿Cómo es posible que los ventiladores nos refresquen, cuando en realidad calientan el aire al moverlo?

Hasta mediados del siglo XIX no se comprendió que el calor es una forma de energía

La revolución relativista obligó a reformular la ley de la conservación de la energía

En realidad, los experimentos de Galileo tenían más que ver con planos inclinados que con torres inclinadas

¿Cuánto tardaría en efectuar una oscilación completa un péndulo con un hilo de 100 metros?

Cuatro acertijos veraniegos de tres grandes maestros y una gran maestra de la matemática recreativa

Muchos acertijos lógico-matemáticos son anónimos, como los chistes, pero otros proceden de ilustres autores

Desde el tradicional tangram hasta los modernos ‘IQ puzzles’, los rompecabezas geométricos han merecido la atención de prestigiosos científicos

No solo seguimos utilizando los números romanos, sino que aún pueden depararnos algunas sorpresas

Puestos a fantasear, ¿qué pasaría si la gravedad fuera distinta de como la conocemos?

En las novelas de Jules Verne encontramos interesantes ejemplos de problemas relacionados con los viajes y los viajeros

‘El mercader de Venecia’ de Shakespeare inspiró algunos de los acertijos lógicos del maestro Raymond Smullyan