Teselas de Penrose

La condición necesaria y suficiente para que un hexágono irregular pueda teselar el plano (ver artículo anterior) es que tenga simetría central, como en el teselado hexagonal achaflanado de la figura. En este caso, las teselas irregulares tienen, además, simetría axial, condición no necesaria, y se combinan con teselas regulares; pero salta a la vista que se puede teselar el plano prescindiendo de los pequeños hexágonos regulares.

En las últimas semanas hemos hablado de teselas y de Penrose, por lo que es inexcusable unir ambos términos y dedicar unos párrafos a las teselas de Penrose.

Todas las teselaciones de las que nos hemos ocupado recientemente, así como la inmensa mayoría de las que podemos ver en mosaicos y embaldosados de todo tipo, son periódicas, lo que significa que podemos delimitar en ellas una región que pavimenta el plano por traslación, es decir, desplazándola sin someterla a giros ni simetrías (una manera informal de decirlo es que el mismo diseño básico se mantiene a lo largo y a lo ancho de todo el teselado).

Los polígonos regulares que pueden teselar el plano -el triángulo equilátero, el cuadrado y el hexágono regular- solo pueden hacerlo de forma periódica; pero con rombos iguales, por ejemplo, podemos realizar teselaciones tanto periódicas -el típico arlequinado- como aperiódicas (¿puedes dibujar alguna?).

Un tipo peculiar de teselaciones aperiódicas son las agrupaciones de teselas que forman copias de sí mismas a mayor escala, que Solomon W. Golomb denominó reptiles (contracción de repetitive tiles, teselas repetitivas), como vimos hace unos meses al hablar de los poliominós.

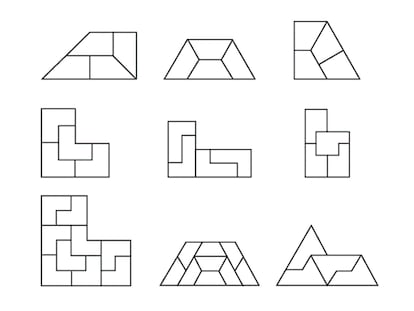
Durante mucho tiempo se pensó que todas las teselas que podían dar lugar a teselaciones aperiódicas, también podían reordenarse en configuraciones periódicas, como en el caso de los rombos o los reptiles; pero a partir de los años setenta del siglo pasado se han descubierto conjuntos de teselas que solo pueden dar lugar a teselaciones aperiódicas, como las seis teselas obtenidas por Raphael M. Robinson a partir del cuadrado, o las seis de Robert Ammann, que vemos en la figura, también a partir del cuadrado.

Pero quien más ha avanzado en este campo es Roger Penrose, reciente Premio Nobel de física, que en 1973 descubrió un conjunto de seis teselas que imponen la teselación aperiódica. En 1974 las redujo a cuatro, y posteriormente las redujo a dos.

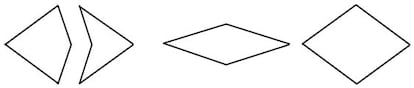
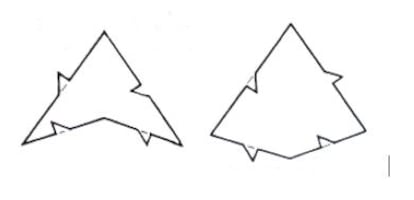
Hay dos parejas de estas teselas de Penrose binarias: una formada por dos rombos de lados iguales, pero ángulos distintos (¿puedes calcularlos?), y otra formada por dos cuadriláteros con simetría axial, uno cóncavo y otro convexo, obtenidos por partición del rombo menos alargado de la pareja anterior, y que John Conway denominó dart y kite (dardo y cometa). Para que el teselado al que pueden dar lugar sea necesariamente aperiódico, hay que imponer ciertas restricciones; de lo contrario, es evidente que con la pareja de rombos se puede realizar un teselado periódico, y que un dardo y una cometa pueden acoplarse reconstruyendo el rombo del que derivan, con el que la teselación periódica es igualmente obvia. Las restricciones pueden materializarse, por ejemplo, coloreando los lados y permitiendo solo la unión de lados del mismo color, o añadiendo salientes y entrantes que limiten las formas de acoplamiento, como se ve en la figura.

Cuasicristales

Los teselados aperiódicos podrían parecer un mero divertimento matemático sin conexión con el mundo real; pero el descubrimiento de los cuasicristales a mediados de los años ochenta del siglo pasado (por el que Dan Shechtman recibió el Premio Nobel de química), mostró que en la naturaleza se forman estructuras ordenadas, pero no periódicas, lo que supuso una auténtica revolución en el campo de la cristalografía. Pero ese es otro artículo.

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.