Adiós a un matemático surrealista y mágico

La pandemia del coronavirus no respeta ni a los dioses del olimpo matemático. El pasado 11 de abril falleció el gran matemático británico John Horton Conway (Liverpool, 1937), en Nueva Jersey, Estados Unidos. Su colega, medalla Fields y premio Abel, sir Michael Atiyah, le describió como “el matemático más mágico del mundo”. Muchas de sus grandes contribuciones científicas nacieron de su gran afición a los juegos.

Mientras que era profesor en Cambridge, entre 1969 a 1970, vivió su gran periodo de inspiración, similar al que experimentaron antes otros grandes científicos como Einstein y Newton. Hizo descubrimientos que llegaron más allá de la comunidad científica, entre los que destaca el famoso juego de la vida. Es un sencillo juego para una persona, que reproduce interesantes analogías con el crecimiento, alternancia y fallecimiento de sociedades de organismos vivos. De esta manera, se considera un juego de simulación, ya que imita el comportamiento de procesos de la naturaleza. Sin embargo, para Conway la motivación de desentrañar el juego era puramente matemática: quería encontrar un sistema universal, capaz de realizar cálculos arbitrarios, si se dispusiese de suficiente tiempo y suficiente memoria, es decir, una especie de ordenador infinitamente programable

Empleaba un tablero (infinito) dividido en cuadrados, como el del conocido juego del Go. Cada posición tiene ocho celdas vecinas: cuatro con lados adyacentes y cuatro en la diagonal con un vértice en común. Cada organismo vivo queda representado por una ficha en una celdilla, y el juego consiste en observar su evolución a lo largo del tiempo, aplicando unas sencillas reglas que determinan los nacimientos, muertes y supervivientes tras cada jugada:

· Supervivientes. Cada ficha con dos o tres vecinos vivos sobrevive al siguiente turno.

· Muertes. Cada ficha rodeada por cuatro o más vecinos muere por superpoblación. Pero también las fichas que tengan solo uno o ningún vecino vivo mueren por aislamiento

· Nacimientos. Cada celda vacía que tenga exactamente tres vecinos –ni más ni menos- se convierte en una celda de nacimiento. En la siguiente generación, en esa celda vacía aparece una nueva ficha.

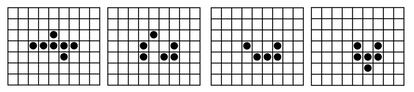
A partir de configuraciones iniciales y reglas muy sencillas surgen patrones extremadamente complicados. Aunque el juego de la vida es completamente determinista no podemos predecir completamente cómo se desarrollarán estas configuraciones a largo plazo, por ejemplo, no podríamos garantizar que vayan a adoptar una configuración predeterminada tras una serie de pasos del juego. Llevando esta analogía al comportamiento humano, podríamos pensar que aunque éste pueda tener un origen determinista simple, no implica que el comportamiento resultante sea siempre predecible.

El juego de la vida de Conway es un ejemplo de autómata celular, es decir, un sistema dinámico que evoluciona en un número de pasos. El primero en idear un sistema de este tipo fue John von Neumann, cuya cátedra ocupó Conway en la Universidad de Princeton en 1986. Los autómatas celulares se han aplicado en ciencia de la computación, física matemática, sistemas complejos, biología, ingeniería… Por ejemplo, están en la base de la computación en paralelo y en el diseño de ordenadores cuya arquitectura esté basada en principios y materiales biológicos.

El juego de la vida de Conway es un ejemplo de autómata celular, es decir, un sistema dinámico que evoluciona en un número de pasos

También pensando en el juego del Go, inventó un nuevo tipo de números, los “números surreales”. En el juego chino, en la estructura de los finales de las partidas se forman diferentes subjuegos, al separarse las fichas restantes en el tablero. Conway observó cómo se podían sumar estos subjuegos y a partir de esta idea describió una nueva clase de números, los números surreales, en los que cada número se define a partir de los anteriores. Además de los números reales, los números surreales contienen números infinitesimales, es decir, números infinitamente pequeños, y otras familias de números infinitos.

Otro de los descubrimientos de Conway durante su annus mirabilis fue el grupo de Conway, que surge al buscar la mejor forma de apilar esferas en dimensión 24, de forma que cada esfera está en contacto con otras 196.560 esferas, lo que supone la configuración “más densa” para esta dimensión.

Sería imposible seguir detallando todos los campos en los que destacó Conway: álgebra, teoría de números, teoría de nudos, combinatoria, probabilidad, análisis… Incluso en mecánica cuántica probó, junto a Simon B. Kochen en 2006, el famoso y sorprendente Teorema del libre albedrío (Will Free Theorem) que afirma, a grandes rasgos, que al igual que los humanos tenemos libre albedrío, también lo tienen las partículas elementales, bajo ciertas hipótesis.

Asistir a las charlas de Conway era una experiencia maravillosa, casi mágica. En Princeton prefería dar las clases de primer curso, las que normalmente nadie quiere dar, porque son demasiado básicas, para persuadir a los estudiantes en convertirse en futuros matemáticos. En los veranos, participaba frecuentemente en campamentos de matemáticas para motivar a las generaciones venideras. Allí se presentaba solamente con una baraja, unas monedas, cuerdas, unos dados y otros utensilios inverosímiles y con ellos era capaz de improvisar y desarrollar ideas matemáticas cautivando a la audiencia.

La vida de Conway fue intensa, con momentos maravillosos y otros muy difíciles, incluido un intento de suicidio, pero lo que siempre perdurará es su mágico legado.

David Martín de Diego es investigador científico del CSIC en el ICMAT y vicepresidente de la Real Sociedad Matemática Española

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (Icmat), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.

Edición y coordinación: Ágata Timón (Icmat).

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aquí a nuestra newsletter.