Teselados pentagonales

Veíamos la semana pasada que los ocho tipos de teselados semirregulares responden a la notación:

3.3.3.3.6, 3.3.3.4.4, 3.3.4.3.4, 3.4.6.4, 3.6.3.6, 3.12.12, 4.6.12, 4.8.8

Los números separados por puntos indican el número de lados de cada uno de los polígonos regulares que confluyen en un vértice, empezando por los de menos lados y en sentido giratorio. Así, 3.4.6.4 significa que en cada vértice del teselado confluyen un triángulo equilátero, dos cuadrados y un hexágono regular, en el orden triángulo-cuadrado-hexágono cuadrado, tal como se ve en la figura.

La notación no indica el tamaño relativo de los polígonos regulares implicados; pero es que para cada combinación solo hay una correlación de tamaños posible.

En cuanto a la posibilidad de teselar el plano con cualquier cuadrilátero y con algunos hexágonos irregulares, nuestro comentarista habitual Luca Tanganelli ha enviado la siguiente reflexión (ilustrada):

“Los cuadriláteros se dividen en triángulos que teselan el plano en “tiras” (líneas discontinuas). Además, se revela un segundo teselado con hexágonos que se obtienen duplicando por simetría rotacional cada cuadrilátero (en rojo). Por lo tanto, que un hexágono se pueda dividir en dos cuadriláteros iguales es condición suficiente para teselar el plano (un hexágono cóncavo también puede teselar); pero si es necesaria no lo sé aún”.

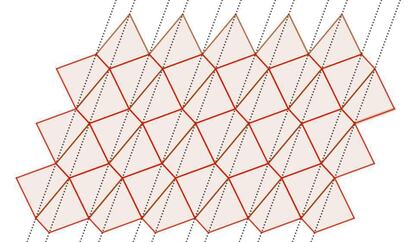
¿Es condición necesaria, para que un hexágono pueda teselar el plano, que pueda dividirse en dos cuadriláteros iguales? Otrosí: ¿De qué otra manera se puede formular la condición necesaria y suficiente?

Teselados pentagonales monoedrales convexos

Es evidente que no se puede teselar el plano con pentágonos regulares, puesto que el ángulo interior de un pentágono regular mide 108º, que no es divisor de 360º (sí que pueden, sin embargo, los pentágonos regulares recubrir una superficie esférica o hiperbólica).

Con algunos pentágonos irregulares es posible teselar el plano, como vimos al hablar del mosaico de El Cairo, el más conocido ejemplo de recubrimiento de una superficie plana mediante piezas pentagonales convexas de la misma forma y tamaño: lo que técnicamente se denomina un teselado pentagonal monoedral convexo.

A lo largo del siglo XX y lo que va del XXI, se han descubierto 15 tipos distintos de estos teselados (el último en fecha tan reciente como 2015), y parece ser que no hay más posibilidades (hay una demostración de imposibilidad pendiente de comprobación, aunque es probable que en el momento de escribir estas líneas ya haya sido comprobada). No es sorprendente que Martin Gardner y su sección de juegos matemáticos de Scientific American desempeñaran un papel importante en esta investigación; pero sí lo es que una matemática aficionada sin ninguna formación universitaria descubriera 4 de los 15 teselados pentagonales monoedrales convexos posibles: es el extraordinario caso de la recientemente fallecida Marjorie Rice (1923-2017), que incluso creó su propia forma de notación operativa y su personal línea de trabajo (desarrollada, como ella misma contó, en la cocina de su casa), y cuya web Intriguing Tessellations merece una visita de mis sagaces lectoras/es.

En la imagen, los 4 tipos de teselado pentagonal descubiertos por Rice, que demostró que un matemático aficionado -y una matemática aficionada- aún puede hacer aportaciones al más alto nivel.

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.