El mosaico infinito

Veíamos la semana pasada que el 300 es un número “abundante”, y que, por la lista de los números abundantes que hay entre los 100 primeros, parecería que todos son pares; pero no es así: hay infinitos números abundantes impares, aunque si los buscamos recorriendo uno a uno la lista de los naturales tardaremos bastante en encontrar el primero y menor de ellos, que es el 945. Para comprobar la infinitud de los números abundantes, tanto pares como impares, basta ver que todos los múltiplos de un número abundante son, a su vez, abundantes (¿por qué?).

Además de abundante, el número 300 es la suma de diez primos consecutivos:

300 = 13 + 17 + 19 + 23 + 29 + 31 + 37 + 41 + 43 + 47

También es un número poligonal: concretamente, 300 es el 24º número triangular.

Teselados irregulares

Hablábamos la semana pasada de teselados regulares y semirregulares, y puesto que en el segundo caso podemos combinar todos los polígonos regulares que queramos, de cualquier tamaño y en cualquier proporción, parecería que las posibilidades son muchas, por no decir ilimitadas; pero no es así si el patrón es regular, es decir, el mismo en cada vértice de la configuración. De hecho, solo hay 8 teselados semirregulares, que se identifican con esta notación:

3.3.3.3.6, 3.3.3.4.4, 3.3.4.3.4, 3.4.6.4, 3.6.3.6, 3.12.12, 4.6.12, 4.8.8

¿Qué significan estos números?

Pero los numerosos mosaicos geométricos que encontramos en todas las épocas y en todas las culturas no se ciñen a los polígonos regulares. Veamos algunos de los formados por un solo tipo de teselas, todas iguales.

Las teselas más abundantes, junto con las cuadradas, son las rectangulares, que vemos en todo tipo de embaldosados y construcciones con ladrillos. Y es evidente que cualquier paralelogramo también puede teselar el plano, pues no tenemos más que prolongar los lados de un paralelogramo seminal y trazar las oportunas paralelas a los mismos, equidistantes entre sí, para formar una malla homogénea.

Y puesto que con todo triángulo se puede formar un paralelogramo adosándole otro triángulo igual, cualquier triángulo puede teselar el plano.

Menos evidente es que con cualquier cuadrilátero, convexo o cóncavo, también se puede teselar el plano. ¿Cómo se demuestra?

Con algunos hexágonos irregulares se puede teselar el plano, pero no con todos. ¿Con cuáles es posible?

La prohibición islámica de reproducir figuras humanas o de otros animales favoreció el desarrollo de una amplia iconografía basada en las figuras geométricas y los patrones repetitivos, como se puede observar en grandes monumentos históricos como la Alhambra (cuyos mosaicos y motivos ornamentales fueron estudiados en profundidad por el grabador neerlandés M. C. Escher). En los mosaicos árabes encontramos figuras habituales en otras culturas, como las estrellas (de 5, 8 o 12 puntas, entre otras) o los rombos, y otras muy características, como un peculiar pentágono con los cinco lados iguales, con dos ángulos rectos, dos de 108º y uno de 144º, que da lugar al denominado mosaico de El Cairo, pues se ve con frecuencia en las calles de la capital egipcia. Se suele redondear, y así lo he hecho, el valor de los ángulos de 108º y 144º, ¿puedes hallar su valor exacto?

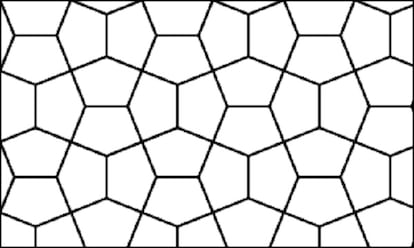
El del mosaico de El Cairo es uno de los 15 pentágonos irregulares con los que se puede teselar el plano. No se ha demostrado (que yo sepa) que no haya ninguno más, por lo que invito a mis sagaces lectoras/es a encontrar un 16º tipo de pentágono teselador, o a demostrar que no existe.

En cuanto al título de esta entrega, ¿podemos tomárnoslo en sentido literal? ¿Es realmente infinito el número de mosaicos posibles?

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aquí a nuestra newsletter