Pentágonos y hexágonos
¿Cuántos pentágonos y hexágonos conforman la superficie de un balón de fútbol?


Como hemos visto en las últimas semanas, la secuencia de los números triangulares es 1, 3, 6, 10, 15, 21…, y la de los cuadrados, 1, 4, 9, 16, 25, 36… ¿Cuál será la secuencia de los números pentagonales?
Conviene empezar señalando que, a diferencia de los números triangulares y cuadrados, los números pentagonales se forman según patrones de contorno.
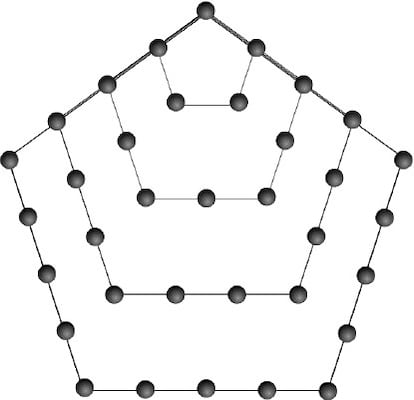
Para hallar, por ejemplo, el quinto número pentagonal, empezamos formando un pentágono regular de 5 puntos de lado, y luego a partir de uno de los vértices, vamos formando sucesivos pentágonos de puntos con ese vértice en común, como se ve en la figura, y de este modo obtenemos los 5 primeros números pentagonales, cada uno de los cuales es la suma de su propio perímetro más los anteriores. Como en el caso de los triangulares, se considera que el primer número pentagonal es el 1 (el vértice común como pentágono de lado 0), así que la secuencia será:
1, 5, 12, 22, 35…
¿Cuál es el sexto número pentagonal?, ¿y el séptimo?, ¿y el décimo? ¿Hay una fórmula general que nos permita hallar el enésimo número pentagonal?
Y, viceversa, dado un número cualquiera, ¿podemos averiguar fácilmente si es pentagonal o no?
Los números hexagonales se construyen igual que los pentagonales, pero formando, en vez de pentágonos, hexágonos sucesivos con un vértice común.
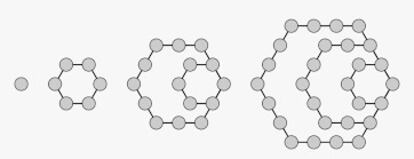
Como se puede ver en la figura, la secuencia es:
1, 6, 15, 28…
¿Cuál es el quinto número hexagonal?, ¿y el sexto?, ¿y el décimo? ¿Hay una fórmula para hallar el enésimo número hexagonal?
Y, viceversa, dado un número cualquiera, ¿cómo podemos averiguar si es hexagonal o no?
El siguiente número poligonal es, obviamente, el heptagonal. La secuencia es:
1, 7, 18, 34, 55, 81, 112, 148, 189, 235…
Y la fórmula para hallar el enésimo número heptagonal es: (5n² – 3n)/2
Aún más sencilla es la fórmula de los números octogonales: 3n² – 2n, cuya secuencia es, por tanto:
1, 8, 21, 40, 65, 96, 133, 176, 225, 280…
La fórmula de los números decagonales es 4n² – 3n, la misma que la de los octogonales con ambos coeficientes aumentados en una unidad. Y la de los números dodecagonales, 5n² – 4n. ¿Qué nos dice esta secuencia de fórmulas?
Vecinos colaborativos
Los pentágonos y los hexágonos, además de ser polígonos sucesivos y dar lugar, por ende, a números poligonales sucesivos, pueden asociarse para recubrir (convenientemente curvados) superficies esféricas, como salta a la vista en el conocido caso del balón de fútbol. El hexágono regular es, junto con el triángulo equilátero y el cuadrado, uno de los tres polígonos regulares que pueden “embaldosar” el plano. El pentágono no puede, pero en asociación con su vecino da pie a otros interesantes recubrimientos.
¿Cuántos pentágonos y hexágonos hacen falta para recubrir la superficie de una esfera? O lo que es lo mismo, ¿de cuántas piezas se compone la envoltura de un balón de fútbol? ¿Es única la solución?
Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.
Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aquí a nuestra newsletter
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































