Rompecabezas geométricos

Los números romances de la semana pasada son una broma veraniega consistente en imaginar cómo “leería” un antiguo romano nuestros números posicionales decimales; para él, el 51 sería un 5 más un 1, o sea, 6. Y el hecho de que la numeración romana (heredera de la etrusca) fuera aditiva y no posicional hace superfluo el 0, que no suma ni resta nada, y cuya utilidad (genial, revolucionaria) es la de indicar que en un determinado lugar de la secuencia posicional no hay ningún elemento (por ejemplo, que en 507 hay 5 centenas, 7 unidades y ninguna decena).

En cuanto al anacrónico (anacrónico para los propios romanos) IIII en lugar de IV, hay diversas teorías; la más difundida es la de que las letras IV son las iniciales de IVPITER, el más importante dios romano, por lo que se consideraba una falta de respeto colocarlo en un reloj (aunque fuera de sol).

Con respecto a la bola de hierro tirada al mar sobre la fosa de las Marianas, hay que tener en cuenta, ante todo, que un objeto que cae en el seno de un fluido -sea aire, agua u otro- alcanza rápidamente una velocidad máxima que, a partir de ese momento, permanece constante, pues la resistencia del fluido aumenta con la velocidad, con lo que pronto llega a un punto de equilibrio con el tirón gravitatorio que tiende a acelerar el objeto.

En el aire, mucho menos denso que el agua, un paracaidista en caída libre se estabiliza al alcanzar una velocidad de entre 200 y 400 kilómetros por hora, según que adopte una posición de frenado o de picado. En el agua, obviamente, la velocidad de caída es mucho menor. Todos hemos visto hundirse un objeto en una piscina (por ejemplo, jugado a buscar una piedra o una moneda tirada al agua), y podemos estimar que desciende unos cuantos metros en un segundo, digamos 10 para redondear, por lo que es razonable pensar que la bola de la semana pasada tardaría del orden de 20 minutos en descender los 11 kilómetros de profundidad de la fosa de las Marianas. Quien quiera efectuar un cálculo más preciso puede recurrir a la ley de Stokes, que suministra una fórmula para calcular la velocidad de caída de una esfera en el seno de un líquido en función de la densidad de aquella y la viscosidad de este.

El cuadrado inteligente

Y nada mejor para amenizar una ociosa jornada veraniega que un clásico rompecabezas geométrico nieto del tangram e hijo de los poliominós, uno de esos que, en inglés, responden a la denominación genérica de IQ puzzles.

Uno de los más conocidos es el IQ square de la figura, analizado, entre otros, por el conocido científico, divulgador e inventor estadounidense Clifford Pickover. Para intentar resolver los interesantes problemas que nos propone este “cuadrado inteligente”, podemos recortar las piezas en un trozo de cartón, o bien intentar componer cada configuración en una hoja de papel cuadriculado (sin descartar la opción de comprar un juego de piezas en una tienda especializada o pedirlas por internet).

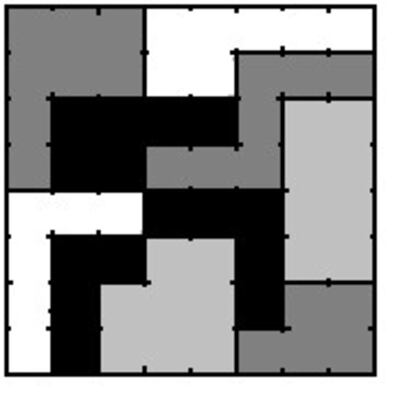
El primer desafío, obviamente, consiste en desordenar las piezas y recomponer el cuadrado. ¿Hay más de una forma de hacerlo?

Más difícil todavía (o tal vez no):

Eliminando una de las 10 piezas, ¿se puede formar un cuadrado con las 9 restantes?

Eliminando 2 de las piezas, ¿se puede formar un cuadrado con las 8 restantes?

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.