
Extrañas coincidencias
¿Cuál es la probabilidad de que, en un grupo de siete personas, dos celebren su cumpleaños la misma semana?

¿Cuál es la probabilidad de que, en un grupo de siete personas, dos celebren su cumpleaños la misma semana?

¿Puedes imaginar un laberinto sin fin? ¿Y uno del que se saliera girando siempre hacia la izquierda?

En su novela ‘Ada o el ardor’, Vladimir Nabokov convierte a Borges en Osberg. ¿Puedes revertir la deconstrucción y devolverle su nombre al escritor argentino?

¿De cuántas maneras distintas puedes doblar un sencillo mapa con dos dobleces verticales y uno horizontal?
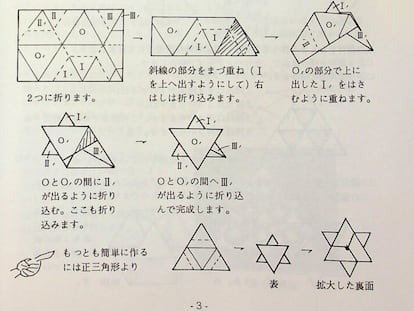
¿Cuántas veces y de cuántas maneras distintas puedes doblar una hoja de papel?

¿Puedes dibujar un pentágono regular sin utilizar una regla graduada? ¿Y un heptadecágono?

Los dos pesos pesados de las matemáticas francesas se enfrentaron en el ring de las coordenadas… ¿cartesianas?

El químico inglés Frederick Soddy redescubrió el teorema de Descartes y lo convirtió en un poema erótico

El vuelo de una mosca le inspiró a Descartes las coordenadas que llevan su nombre

Además de sus contribuciones a la teoría de diseños combinatorios, Jakob Steiner fue uno de los más grandes geómetras de todos los tiempos
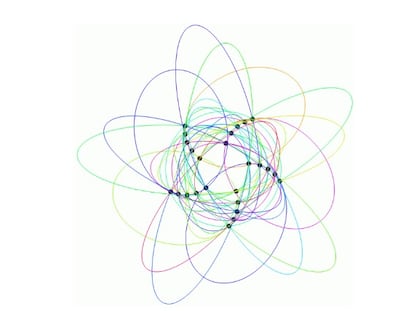
Tanto la sextina como el problema de las colegias y otros similares tienen que ver con la teoría del diseño combinatorio

En la singular estructura de la sextina confluyen la poesía y las matemáticas

Las combinaciones de letras, personas u otros elementos y la autorreferencia son inagotables fuentes de problemas y paradojas

Al igual que la vida, las palabras surgen de una sopa (de letras) primordial y una combinatoria inagotable

Mediante la teoría de grafos, la torre de Hanói también se relaciona con el triángulo de Sierpinski
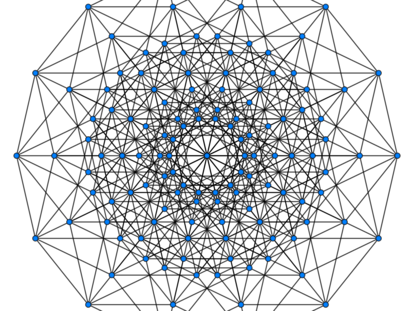
Existe una sorprendente correspondencia entre una torre de Hanói de ‘n’ discos y un hipercubo ‘n-dimensional’

Objetos matemáticos en apariencia muy distintos pueden estar relacionados de maneras sorprendentes
A veces coinciden y a menudo se confunden, pero los caminos ‘eulerianos’ y los caminos ‘hamiltonianos’ son distintos

El conocido como triángulo de Pascal o de Tartaglia es muy anterior a ambos matemáticos europeos, y fue estudiado en Persia ya en el siglo XI

El 2024 es el vigésimo segundo número piramidal triangular y se puede representar como un gran tetraedro de esferas apiladas

La cifra del año 2024 no da mucho juego desde el punto de vista matemático, pero su terminación, el 24, no tiene desperdicio

Un sobrecogedor relato de Edgar Allan Poe sirve de base a un intrigante acertijo lógico

Hay decisiones que no parecen dudosas, como la de elegir entre un tigre hambriento y una hermosa dama, y sin embargo…

Los sólidos platónicos no son los únicos poliedros con todas las caras iguales

El matemático alemán Charles Proteus Steinmetz, además de estudiar los sólidos que llevan su nombre, hizo importantes contribuciones en el campo de la ingeniería eléctrica

Gaspard Monge, matemático francés amigo de Napoleón, fue el creador del sistema diédrico para la representación plana de objetos tridimensionales

Napoleón fue un gran amante de las ciencias en general y de las matemáticas en particular, e incluso se le atribuyen algunas contribuciones relevantes

¿Por qué para los físicos son “mágicos” los números 2, 8, 20, 28, 50, 82 y 126?

Descartes los denominó así despectivamente, pero se convertirían en una herramienta muy real de las matemáticas

¿Cuánto tiempo tardan los fotones generados en el centro del Sol en alcanzar su superficie y salir al vacío?

La teoría de la decisión, ligada al cálculo de probabilidades, da lugar a interesantes paradojas

La extracción de bolas al azar no solo puede dar lugar a paradojas de la probabilidad, sino también de la teoría de la decisión

Además de ser un físico de primera fila, George Gamow fue un excelente narrador, como se aprecia en sus libros de divulgación y de matemática recreativa

Los problemas de optimización relativos al uso de ascensores dan lugar a curiosas paradojas e ingeniosos algoritmos

Entre los numerosos medios de transporte que aparecen en los problemas de matemática recreativa, no podían faltar los ascensores

Algunos números muy importantes son conocidos y accesibles, como π o e, pero otros, como la constante de Chaitin, son ignorados y difíciles de entender por los no matemáticos
He aquí algunos candidatos a añadir a la lista de los números más interesantes

Todos los números son interesantes, pero algunos lo son de una manera muy especial

Pappus de Alejandría formuló importantes teoremas geométricos y estudió los sólidos platónicos en relación con la esfera

Según determinadas configuraciones, plantar árboles es un tema clásico de los problemas de ingenio