Un paseo por la cuarta dimensión

La “moraleja” del famoso problema de los nueve puntos, del que nos ocupábamos (y no por primera ni última vez) la semana pasada, es que a veces, sin darnos cuenta, nos imponemos más condiciones de las que se establecen en el planteamiento. En el caso que nos ocupa, al ver nueve puntos dispuestos en una cuadrícula, tendemos a dar por supuesto que una línea quebrada que los una también estará encerrada en la cuadrícula, o, dicho de otro modo, que todos sus vértices coincidirán con algunos de los nueve puntos.

En el problema de la división de un triángulo obtusángulo en acutángulos, aunque aparentemente no tenga nada que ver con el anterior, es frecuente autoimponerse una restricción análoga: en este caso, que todos los vértices de los acutángulos sean puntos del perímetro del obtusángulo, y con esta condición autoimpuesta la división no es posible; pero sin esta restricción innecesaria se puede dividir un triángulo obtusángulo en… ¿cuántos acutángulos como mínimo?

Con respecto al clásico de los cuatro árboles equidistantes, esto es lo que dice nuestro “usuario destacado” Salva Fuster: “En el problema de los cuatro árboles en los que cada uno de ellos dista lo mismo de los otros tres, me parece que tenemos diferentes alternativas según el terreno, la forma de los árboles y la definición de distancia entre ellos. Por ejemplo, si el terreno es plano y tomamos la distancia entre dos árboles como la que hay entre sus centros de masa, podríamos tener un árbol de poca (mucha) altura rodeado de otros tres más altos (bajos) de manera que los centros de masa de los cuatro árboles formen un tetraedro. Si la distancia entre dos árboles se considera la de la mínima distancia entre cualquier punto de ellos, podemos tener cuatro árboles a la misma distancia a diferentes alturas, o incluso sencillamente estando en contacto entre todos ellos”.

La solución clásica es que hay un montículo en el terreno: uno de los árboles se planta en lo alto del mismo y los otros tres a su alrededor y a menor altura, de forma que los cuatro estén en los vértices de un tetraedro regular.

Y para formar cuatro triángulos equiláteros con seis cerillas también hemos de saltar del plano al espacio y recurrir al tetraedro; de ahí su analogía con el problema de los árboles, con el que aparentemente no tiene nada que ver.

Aunque, si se permite que las cerillas se crucen, sí que hay una solución plana. ¿Cuál es?

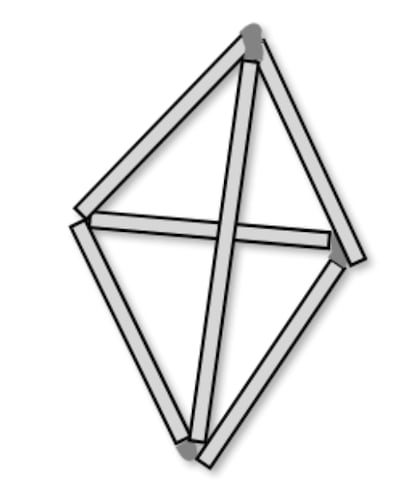
Hipersólidos platónicos

¿Y si tuviéramos que plantar cinco árboles equidistantes en vez de cuatro? En ese caso tendríamos que trasladarnos a la cuarta dimensión y situar los árboles (o los hiperárboles) en los vértices de un pentácoron, el más sencillo de los politopos regulares tetradimensionales (denominados polícoros).

Como seres tridimensionales que somos (sin contar la dimensión temporal ni posibles dimensiones extra vestigiales, como las propuestas por la teoría de cuerdas), no podemos concebir cuerpos tetradimensionales, pero sí que podemos deducir sus características. Vamos a ver si es verdad:

¿Cuántas aristas tiene el pentácoron? ¿Cómo son sus caras y cuántas son?

Más difícil todavía:

Un politopo no solo tiene vértices (adimensionales), aristas (unidimensionales) y caras (bidimensionales); también tiene “celdas” tridimensionales, como los ocho cubos que envuelven (es un decir) el hipercubo (también denominado octácoron o teseracto), cuyo desarrollo hizo famoso Dalí con uno de sus cuadros (Corpus Hypercubus, 1954).

¿Cuántas celdas tiene un pentácoron y cómo son?

Además del pentácoron y el hipercubo, hay otros cuatro politopos regulares de cuatro dimensiones, casi tan difíciles de nombrar como de concebir: hexadecácoron, icositetrácoron, hecatonicosácoron y hexacosícoron. Los cinco primeros pueden considerarse los análogos tetradimensionales de los sólidos platónicos, mientras que el hexacosícoron, con sus 1.200 caras triangulares y sus 600 celdas tetraédricas, no tiene un equivalente tridimensional. No intentes dibujarlo.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.