Acertijos de autor

Cada entrega de “El juego de la ciencia” suele empezar con las soluciones y posible discusión de los problemas de la semana anterior; pero en este caso, debido por una parte a la pausa veraniega y, por otra, a algunas dificultades recientes con la sección de comentarios, me limitaré a proponer cuatro acertijos —eso sí, todos ellos muy interesantes e instructivos— pergeñados por otros tantos especialistas:

• Asisto con mi pareja a una reunión en la que hay otras cuatro parejas. Al saludarnos se produce un cierto número de apretones de manos. Naturalmente, nadie le da la mano a su pareja ni se la da más de una vez a una misma persona. Terminada la fase de los saludos, le pregunto a cada una de las personas presentes, incluida mi pareja, cuántas manos ha estrechado, y las respuestas que recibo son todas distintas. ¿A cuántas personas ha estrechado la mano mi pareja?

El autor de este elegante acertijo es Lars Bertil Owe, del que lo único que sé es que es sueco (agradeceré cualquier información al respecto que puedan suministrarme mis sagaces lectoras/es).

Determina la veracidad o falsedad de cada uno de los siguientes enunciados:

• Uno y solo uno de los enunciados de esta lista es falso.
• Dos y solo dos de los enunciados de esta lista son falsos.
• Tres y solo tres de los enunciados de esta lista son falsos.
• Cuatro y solo cuatro de los enunciados de esta lista son falsos.
• Cinco y solo cinco de los enunciados de esta lista son falsos.
• Seis y solo seis de los enunciados de esta lista son falsos.
• Siete y solo siete de los enunciados de esta lista son falsos.
• Ocho y solo ocho de los enunciados de esta lista son falsos.
• Nueve y solo nueve de los enunciados de esta lista son falsos.
• Diez y solo diez de los enunciados de esta lista son falsos.

En la versión original de este problema, propuesto por David L. Silverman en el número de enero de 1969 del Journal of Recreational Mathematics, los enunciados, para conmemorar el nuevo año, eran 1969; pero, por razones de espacio, me ha parecido conveniente reducirlos a una decena.

• Sobre una mesa, boca arriba, hay tres cartas sacadas de una baraja de póker dispuestas en fila. A la derecha de un rey hay una o dos reinas. A la izquierda de una reina hay una o dos reinas. A la izquierda de un corazón hay una o dos picas. A la derecha de una pica hay una o dos picas. ¿De qué cartas se trata?

Este ambiguo acertijo es obra del arquitecto Gerald L. Kaufman, autor de The Book of Modern Puzzles y otros libros de pasatiempos lógicos.

Para terminar, en una recopilación de acertijos “de autor” no podía faltar uno de Sam Loyd, uno de los más prolíficos inventores de pasatiempos lógicos, matemáticos y ajedrecísticos de todos los tiempos:

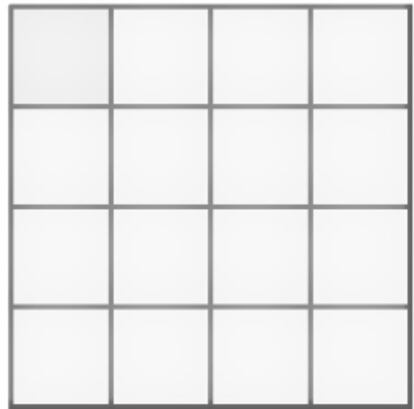
• Imaginemos que la cuadrícula de 4x4 de la figura está formada por 40 cerillas, palillos u otras piezas móviles. ¿Cuántas piezas tenemos que retirar, como mínimo, para que no quede ningún cuadrado? No solo no puede quedar entero ninguno de los 16 cuadrados de 1x1, sino tampoco ninguno de los 9 cuadrados de 2x2, ninguno de los 4 cuadrados de 3x3, ni, por supuesto, el cuadrado total de 4x4. (Obsérvese que el enunciado de este problema contiene la solución de otro muy conocido: ¿cuántos cuadrados hay en la figura?).

Una interesante e instructiva forma de abordar el problema es empezar por cuadrículas más simples. En el caso trivial de un cuadrado de 1x1, es obvio que basta con retirar un palillo. Y en el caso de una cuadrícula de 2x2, es fácil demostrar que hay que retirar 3 palillos para destruir todos los cuadrados. Y en el caso de una cuadrícula de 3x3…

Dadas las altas temperaturas reinantes, se recomienda no intentar resolver estos acertijos a pleno sol ni durante las horas de máximo calor.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.