La rueda de Aristóteles
El funcionamiento de la rueda, elemento clave de la tecnología desde hace miles de años, da lugar a interesantes paradojas


Con respecto al desconcertante fenómeno de las ruedas que en algunas películas parecen girar al revés, mencionado la semana pasada, esto es lo que comenta nuestro “usuario destacado” Rafael Granero:
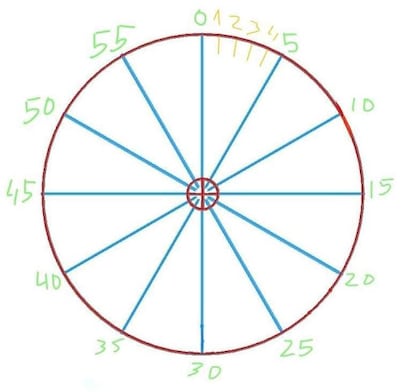
Sea una rueda con 12 radios, de circunferencia 60 cm. Sea un cámara que toma y proyecta “n” imágenes por segundo. Para n = 10, si la rueda gira hacia la derecha o a la izquierda a 50 cm/s, la imagen proyectada por la cámara será estática. Para n = 10, si la rueda gira hacia la derecha a 40 cm/s, la imagen proyectada por la cámara parecerá que retrocede (gira a la izquierda) a 10 cm/s (ver nota bene). Para n = 10, si la rueda gira hacia la derecha a 10 cm/s, la imagen proyectada por la cámara parecerá que avanza (gira a la derecha) a 10 cm/s.
Para n = 10, si la rueda gira hacia la derecha a 25 cm/s, la imagen proyectada por la cámara parecerá que avanza o retrocede o hace las dos cosas alternativamente a 25 cm/s. Nota bene: el radio 5 en 0″ estará en 5; el radio 0 pasado 1/10″ estará en 4 (habrá avanzado 4 cm); el radio 55, pasado 2/10″ estará en 3; el radio 50, pasado 3/10″, estará en 2; el radio 45, pasado 4/10″, estará en 1; el radio 40, pasado 5/10″, estará en 0. La interpretación mental de la proyección es que el radio 5 (y el 10, 15, 20, 25...) ha recorrido 5 cm hacia la izquierda en 1/2″.
Ruedas problemáticas
No se puede hablar de ruedas paradójicas, como las que en algunas películas parecen girar al revés, sin mencionar la paradoja de la rueda de Aristóteles. En última instancia, estamos hablando de aritmética modular, una de las grandes aportaciones de Gauss a la matemática (ver La aritmética del reloj, 9 6 2023): lo que cuenta es el resto de la razón entre la velocidad de rodaje/proyección de la película y la velocidad de la rueda.
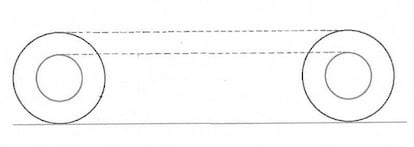
En la figura vemos, en esquema, dos ruedas concéntricas soldadas entre sí (o también podemos pensar en un neumático y su llanta). Al rodar, dando una vuelta completa, desde la posición de la izquierda hasta la de la derecha, cada punto de la circunferencia de la rueda mayor habrá estado en la línea discontinua superior, cuya longitud es igual a la de la circunferencia. A la vez, cada punto de la circunferencia de la rueda menor habrá estado en la línea discontinua inferior, y, como ambas líneas son iguales, ambas circunferencias tienen la misma longitud, lo cual es obviamente falso. ¿Dónde está la falacia?
Galileo, Descartes y Fermat, entre otros, estudiaron esta sutil paradoja, para cuya resolución satisfactoria hubo que esperar a los nuevos desarrollos de la matemática propiciados por el cálculo infinitesimal y los números transfinitos de Cantor. Y hablando de los puntos de contacto de una circunferencia que gira, he aquí un curioso problema aparecido en The American Mathematical Monthly en 1960, en pleno auge de la moda del hula-hop:
Una chica cuya cintura es una circunferencia perfecta hace rodar un aro de hula-hop cuyo diámetro es el doble que el de su cintura. Cundo el punto del aro que está en contacto con el ombligo de la chica vuelva a la posición onfálica, ¿qué distancia habrá recorrido? Y, para terminar, un acertijo del físico estadounidense Stephen Barr, citado por Martin Gardner en uno de sus maravillosos libros de matemática recreativa: ¿Qué tipo de transporte o vehículo tiene ocho ruedas y no contamina la atmósfera?
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































