Caminos de celosía

¿Cuál es el quinto número de Motzkin?, nos preguntábamos la semana pasada. He aquí la respuesta de Manuel Amorós: “Vamos a razonar para obtener de forma recursiva M(5), el número de Motzkin para 5 puntos. Consideremos un vértice determinado V. Pueden pasar dos cosas: desde ese vértice sale alguna cuerda o no sale ninguna. En el segundo caso dicho vértice no interviene en las formas de unir los cuatro puntos que quedan, y por tanto tenemos M(4) opciones. Si una cuerda sale de V dividirá el círculo en dos partes independientes, ya que no podemos atravesarla. Podemos combinar las posibilidades a ambos lados, que son a su vez números de Motzkin, donde se descuentan los dos vértices de la cuerda separatoria. Resumiendo: M(5) = M(4) + M(0)*M(3) + M(1)*M(2) + M(2)*M(1) + M(3)*M(0). Sustituyendo los valores conocidos M(0) = 1, M(1) = 1, M(2) = 2, M(3) = 4, M(4) = 9, obtenemos: M(5) = 9 + 4 +2 + 2 + 4 = 21″.

Al igual que ocurre con los números de Delannoy, no hay una fórmula sencilla que dé M(n) en función de n, hay que utilizar sumatorios o integrales (o hallarlos por recurrencia, como acabamos de ver).

En cuanto a la relación de los números de Motzkin con los de Delannoy, tiene que ver con los posibles recorridos efectuados en una cuadrícula de acuerdo con ciertas reglas, es decir, con los denominados genéricamente “caminos de celosía” (lattice paths en inglés).

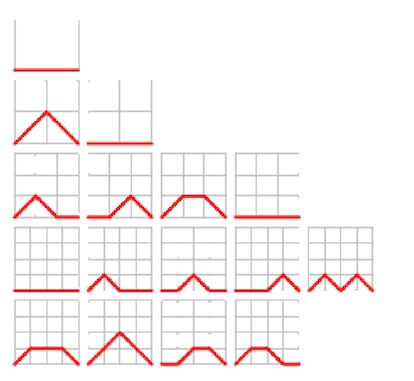
¿De cuántas maneras distintas podemos ir del vértice inferior izquierdo al vértice inferior derecho de una cuadrícula de n x n en n pasos, si los pasos son lados o diagonales de las casillas?

En la figura vemos las distintas posibilidades para las cuadrículas de 1 x 1 (1 camino), 2 x 2 (2 caminos), 3 x 3 (4 caminos) y 4 x 4 (9 caminos). Y, sí, son los números de Motzkin, definidos de una manera distinta a como lo hicimos anteriormente y muy similar a como se definen los números de Delannoy: ambos tipos de números son variantes de los caminos de celosía.

A este respecto, comenta Bretos Bursó: “No sé ver la relación que sugiere Carlo entre los números (o caminos) de Delannoy y los de Motzkin, pero sé una forma bonita de sacar los números de Motzkin. En el triángulo de arriba cada número es suma del que tiene encima y el que tiene encima a la izquierda (es el de Pascal, claro). En el de abajo, cada número es suma de los que tiene encima, encima a la derecha y encima a la izquierda, y la primera columna es la de los números de Motzkin”.

Números de Narayana

No se puede hablar de los números de Delannoy y los de Motzkin sin mencionar los de Narayana (denominados así en honor del matemático canadiense de origen indio T. V. Narayana). Al igual que los de Delannoy, un número de Narayana se define en función de dos naturales: N(m, n), donde n es menor o igual a m.

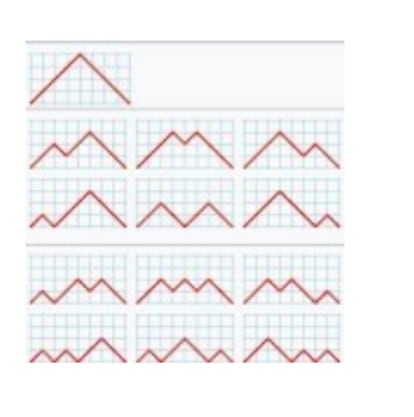
Y al igual que los de Delannoy y los de Motzkin, los números de Narayana representan los distintos caminos posibles que permiten recorrer una cuadrícula de acuerdo con determinadas reglas. Sabiendo que en la figura están representados los números de Narayana N(4, 1) = 1, N(4, 2) = 6 y N(4, 3) = 6, ¿puedes hallar N(4, 4)?

Por cierto, no hay que confundir a T. V. Narayana (1930-1987) con Narayana Pandita (1340-1400), otro ilustre matemático indio famoso por el problema de las vacas de Narayana, parientes cercanas de los conejos de Fibonacci. Pero ese es otro artículo.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.