Palabras y árboles

¿De cuántas maneras distintas se puede dividir un hexágono convexo en triángulos mediante diagonales que no se corten?, nos preguntábamos la semana pasada.

Y la respuesta es 14, o sea, el número de Catalan (Cn) correspondiente a n = 4. De hecho, una de las distintas maneras de interpretar los números de Catalan es definir Cn como el número de maneras distintas de dividir en triángulos un polígono convexo de n + 2 lados mediante diagonales que no se corten. Si n = 4, n + 2= 6, luego el polígono a dividir es un hexágono.

Si las diagonales pueden cortarse, el número de triángulos resultantes es obviamente mayor. He aquí lo que dice Salva Fuster al respecto:

“Si podemos trazar diagonales que se crucen en un polígono convexo, me parece que el número máximo de triángulos que se puede conseguir en un pentágono es de 2 x 5 = 10. Aunque variemos la forma del pentágono, siempre tendremos una zona central en forma de pentágono y 10 triángulos que la rodean. En el caso del hexágono no ocurre lo mismo, pues para el hexágono regular tendremos 3 x 6 = 18 triángulos que rodean una zona central formada por 6 cuadriláteros, pero variando la forma del hexágono podríamos conseguir un triángulo adicional, como se puede ver en la figura adjunta”.

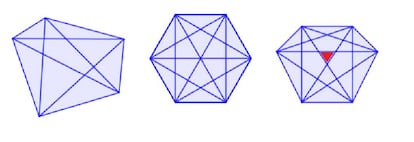
Conviene recalcar que todo lo anterior se refiere a polígonos convexos, que son aquellos cuyos ángulos interiores miden, todos ellos, menos de 180º. Si un polígono tiene algún ángulo interior mayor de 180º, es cóncavo. Pero ¿cuántos ángulos mayores de 180º puede tener un cuadrilátero, un pentágono, un hexágono…? ¿Hay alguna fórmula que nos dé el número máximo de ángulos cóncavos posibles en función del número de lados?

En cuanto al problema “fordiano” de los tres círculos tangentes entre sí y a una recta, Bretos Bursó ofrece la siguiente solución:

“Dados dos números naturales coprimos, m menor que n, los tres radios siguientes son una solución (ordenados de menor a mayor):

m² n², (m + n)² m², (m + n)² n²

Y cualquier otra solución es un múltiplo de alguna de ellas.

En particular, la menor solución (m = 1, n = 2) es la de radios 4, 9 y 36″.

Palabras de Dyck y árboles binarios

Volviendo a los números de Catalan, hay otras muchas maneras de interpretarlos, además de la que acabamos de ver relativa a las diagonales de un polígono. Los siguientes problemas pueden conducirnos a otras tantas interpretaciones/definiciones de los números de Catalan:

1. Dada una cuadrícula de 3 x 3, ¿por cuántos caminos distintos podemos ir de un vértice al opuesto recorriendo los lados de las casillas?
2. Un palabra de Dyck es una cadena de ceros y unos (o de X e Y) con el mismo número de ceros y de unos y en las que ningún subsegmento inicial (es decir, ningún prefijo de la cadena) tiene más unos que ceros. Solo hay una palabra de Dyck de longitud 2: 01; hay dos palabras de Dyck de longitud 4: 0011, 0101. ¿Cuántas palabras de Dyck hay de longitud 6?
3. ¿Cuántos árboles binarios distintos se pueden formar con 7 nodos? Recordemos que en un árbol binario cada nodo solo puede ramificarse en dos como máximo.

Y la metapregunta de rigor: ¿qué tienen que ver estos tres problemas con los números de Catalan?

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.