2023!

La relación de los números de Narayana con los de Catalan, planteada la semana pasada, es sencilla y directa:

Cn = N(n, 1) + N(n, 2) + N(n, 3) + … + N(n, n)

Como vimos, con sus correspondientes gráficos, N(4, 1) + N(4, 2) + N(4, 3) + N(4, 4) = 1 + 6 + 6 + 1 = 14, que es precisamente C4. Y la relación de los números de Narayana con las palabras de Dyck es aún más directa (¿cuál es?).

En la figura vemos los tres árboles enraizados ordenados de cuatro aristas y dos hojas que completan, junto con los 3 de la semana pasada, los 6 posibles, número que se corresponde con N(4, 2). En general, hay N(n, k) árboles enraizados de n aristas y k hojas.

La secuencia de Narayana

En cuanto al problema de las vacas de Narayana, nuestras protagonistas de la semana pasada, si empezamos con una ternera recién nacida a principios del primero año, durante tres años solo tendremos una vaca. El cuarto año la ternera se habrá convertido en vaca adulta y tendrá una cría, y otra al quinto año, y otra al sexto. Al comienzo del séptimo año la primera cría ya estará madura, por lo que nacerán dos terneras (la de la vaca originaria y la de su primera hija), y así sucesivamente. Obtenemos, así, la secuencia:

1, 1, 1, 2, 3, 4, 6, 9, 13, 19…

Es parecida, pero no igual, a la de Fibonacci:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55…

La segunda crece más deprisa (ya se sabe, las conejas son mucho más prolíficas que las vacas), pues cada término es la suma de los dos anteriores, mientras que en la primera cada término es… ¿Cómo expresarías cada término de la secuencia de Narayana en función de los anteriores? ¿Cuál sería el vigésimo término de la secuencia? ¿Cuántas vacas tendríamos en total al cabo de 20 años?

En el problema, tal como lo planteó Narayama Pandita, se supone que todas las vacas viven a lo largo de todo el proceso, lo que significa que la primera vaca vivirá al menos 20 años, una estimación optimista pero verosímil. Más pesimista, nuestro comentarista habitual Francisco Montesinos plantea una variante en la que las vacas solo viven 7 años (ver comentario 9 de la entrega anterior). ¿Cuántas vacas habría, en ese caso, al cabo de 20 años?

En un interesante artículo (la referencia la daré la semana que viene) encuentro esta tabla:

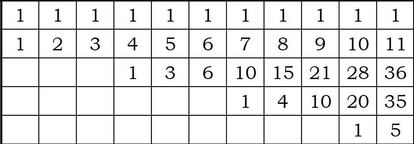
¿Tiene algo que ver con el tema que nos ocupa? ¿Qué significa?

Un gran 2023!

Salvo error u omisión, esta entrega de El juego de la ciencia (la número 395 en EL PAÍS) se publicará el 30 de diciembre, a las puertas del año 2023, por lo que no está de más echarle una ojeada al número como tal. A primera vista, no parece muy interesante: no es primo, no es perfecto, no es poligonal, no es regular, no es factorial, no es un número de Fibonacci ni de Catalan… Podría parecer esfénico, pues es el producto de tres primos: 2023 = 7 x 17 x 17, pero el 17 está repetido, así que tampoco. ¿Pueden mis sagaces lectoras y lectores descubrir alguna propiedad poco evidente de este número que nos acompañará durante 365 días? En cualquier caso, os deseo un gran año en todos los aspectos.

Por cierto, al omitir el signo de admiración inicial en “Un gran 2023!”, no queda claro si os estoy felicitando el año nuevo a la italiana o aludiendo al tamaño del factorial de 2023. ¿De qué orden es 2023!? ¿Con cuántos ceros termina? ¿Cuál es su primera cifra?

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.