Árboles y caminos

¿Cuántos ángulos interiores mayores de 180º puede tener un polígono en función de su número de lados?, nos preguntábamos la semana pasada.

Un triángulo no puede tener ninguno; salta a la vista, pero como a veces la vista nos engaña, digamos que, puesto que los ángulos interiores de cualquier triángulo suman 180º, para que hubiera un ángulo de más de 180º la suma de los otros dos tendría que ser negativa, lo cual es imposible (al menos en el marco de la geometría euclídea).

Un cuadrilátero cóncavo puede tener un solo ángulo mayor de 180º, y un pentágono puede tener dos. ¿Cuántos ángulo cóncavos puede tener, como máximo, un hexágono, un heptágono, un octógono…?

Hay varios caminos (¿cuántos?) por los que se puede ir de un vértice al opuesto de una cuadrícula de 3 x 3 recorriendo los lados de las casillas y en el menor número de pasos posible (“caminos monótonos”, que partiendo del vértice inferior izquierdo van hasta el superior derecho dando solo pasos hacia arriba y hacia la derecha). Si ponemos la condición adicional de que los caminos no crucen la diagonal de la cuadrícula, el número se reduce a 5, que es el número de Catalan C₃, y lo mismo ocurre con las cuadrículas de n x n para cualquier valor de n: el número de caminos monótonos distintos y que no cortan la diagonal es siempre Cn.

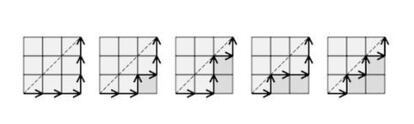
Cn también es el número de árboles binarios de n + 1 nodos sin hijos (denominados hojas o nodos externos) en los que cada nodo tiene 2 hijos o ninguno. En la imagen vemos un árbol binario de este tipo con 4 hojas, luego habrá C₃ = 5 árboles distintos. ¿Puedes dibujarlos todos? ¿Y en el caso de árboles con 5, 6, 7… hojas?

En cuanto a las palabras de Dick, hay 5 de longitud 6:

000111

001011

010011

001101

010101

En general, hay Cn palabras de Dick de longitud 2n; en este caso, como 2n = 6, el número de palabras distintas es C₃ = 5 (¿y qué pasa con las palabras de longitud impar?).

Números de Delannoy

Para ir paso a paso de un vértice al opuesto de una cuadrícula podemos seguir un “camino monótono”, como acabamos de ver, que es una de tantas maneras (hay consignadas más de sesenta, ¿se te ocurre alguna diferente de las que ya hemos visto?) de llegar a los números de Catalan. Si además de los pasos hacia arriba y hacia la derecha se admiten también los pasos en diagonal ascendente (o sea, en dirección norte, este o noreste), tenemos los caminos de Delannoy, llamados así en honor del oficial del ejército francés y matemático aficionado Henri Delannoy (1833-1915). El número de caminos de Delannoy distintos que en una cuadrícula de m x n permiten ir de la esquina suroeste (0, 0) a la esquina noreste (m, n) es el número de Delannoy para esa cuadrícula y se representa como D (m, n).

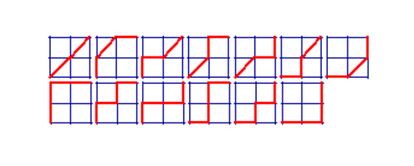
En la imagen vemos los 13 caminos de Delannoy diferentes para una cuadrícula de 2 x 2: D(2, 2) = 13. ¿Cuál es el número de Delannoy para una cuadrícula de 2 x 3? ¿Y para una de 3 x 3? ¿Puedes hallar una fórmula general que dé el número D (m, n) en función de m y n?

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.