Números esfénicos
Los productos y sumas de dos o tres primos son un filón inagotable de la teoría de números


Los 20 primeros términos de la sucesión de las vacas de Narayana, puesto que siguen la pauta V(n) = V(n-1) + V(n-3) —muy similar a la de Fibonacci, en la que F(n) = F(n-1) + F(n-2)— son los siguientes:
1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60, 88, 129, 189, 277, 406, 595, 872…
Por lo tanto, al comienzo del año 21 habrá 872 + 406 = 1278 vacas.
La tabla “mutilada” de la semana pasada, completa, es esta:
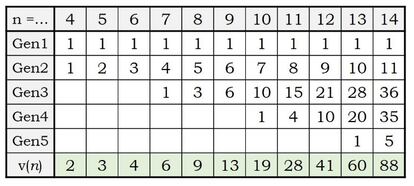
Está tomada de un excelente artículo de Rafael Ibáñez en el Cuaderno de Cultura Científica de UPV/EHU, y muestra que la segunda generación de vacas se corresponde con la sucesión de los números naturales (1, 2, 3, 4, 5…); la tercera, con la sucesión de los números triangulares; la cuarta, con la de los números tetraédricos…
Esfénicos y semipimos
Es probable que al leer el título te hayas acordado del hueso esfenoides. Y es que el nombre del hueso y el de los números comparten etimología: del griego sphen, que significa cuña (en el caso del hueso craneal, el nombre está justificado porque tiene forma de cuña; pero ¿por qué los números esfénicos se llaman así?).
Como vimos la semana pasada, 2023 es casi esfénico, porque es el producto de tres primos: 2023 = 7 x 17 x 17; pero el 17 está repetido, y los números esfénicos son producto de tres primos diferentes. El menor de ellos, por tanto, es 2 x 3 x 5 = 30; y el más grande conocido es el producto de los tres primos mayores, producto que, por el momento, es del orden de 2 elevado a la potencia 123 millones.
Y hablando de números enormes, 2023!, aunque no sea ni remotamente comparable a nuestro esfenicus maximus, tampoco es manco: es un número de 5812 dígitos, cuya primera cifra es un 3 (¿por qué?) y terminado en muchos ceros, cuyo número exacto nos da Manuel Amorós: “Para hallar el número de ceros de 2023! basta calcular la parte entera de 2023/5 + p. e. 2023/5² + p. e. 2023/5³ + p. e. 2023/5⁴ = 404 + 80 + 16 + 3 = 503″.

La sucesión de los números esfénicos comienza así:
30, 42, 66, 70, 78, 102, 105, 110, 114, 130, 138, 154…
Es fácil comprobar que todos estos números tienen exactamente ocho divisores (incluyendo el 1 y el propio número), ¿por qué?
Puede haber dos números esfénicos consecutivos, como 230 = 2 x 5 x 23 y 231 = 3 x 7 x 11 (¿puedes encontrar otra pareja?), e incluso tres: 1309 = 7 x 11 x 17, 1310 = 2 x 5 x 131 y 1311 = 3 x 19 x 23; pero no puede haber cuatro números esfénicos consecutivos, ¿por qué?
Y al hablar de los números esfénicos es obligado mencionar también los semiprimos (denominados también biprimos), que son producto de dos primos (que pueden ser iguales, al contrario de lo que ocurre con los números esfénicos, cuyos tres factores han de ser distintos).
Los semiprimos menores de 100 son:
4, 6, 9, 10, 14, 15, 21, 22, 25, 26, 33, 34, 35, 38, 39, 46, 49, 51, 55, 57, 58, 62, 65, 69, 74, 77, 82, 85, 86, 87, 91, 93, 94, y 95
Como hemos visto al hablar de criptografía, los grandes semiprimos son utilizados frecuentemente para cifrar mensajes, dada la dificultad de descomponer en sus factores el producto de dos primos muy grandes.
En 1966, a vueltas con la conjetura de Goldbach, el matemático chino Chen Jingrun demostró que todo número par suficientemente grande puede expresarse como suma de dos primos o como la suma de un primo y un semiprimo. Pero ese es otro artículo.
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































