Cajas enigmáticas
Los problemas probabilísticos y geométricos con cajas constituyen un inagotable filón de la matemática recreativa
Los enigmáticos ‘Repfigit’
La famosa sucesión de Fibonacci ha servido de base a numerosas construcciones numéricas
Probabilidades paradójicas
Las paradojas probabilísticas aparecen por todas partes, desde una familia numerosa hasta una partida de bridge
Probabilidades sorprendentes
Como hemos visto en semanas anteriores, el cálculo de probabilidades es un venero inagotable de problemas y sorpresas
Números vampiros
De los números narcisistas y vanidosos de las últimas semanas a los vampíricos, que a su vez evocan la cuestión de la persistencia
Números vanidosos
Hay números que, sin ser narcisistas propiamente dichos, parecen gustarse tanto a sí mismos como para poder ser calificados de vanidosos
Números narcisistas
Hay números que parecen gustarse a sí mismo tanto como el mítico Narciso
El enigmático Dr. Matrix
El misterioso personaje creado por Martin Gardner es una fuente inagotable de acertijos numéricos
Teselas de Penrose
El reciente premio Nobel de Física Roger Penrose es, además, uno de los más brillantes e imaginativos matemáticos de nuestro tiempo
Teselados pentagonales
La reciente historia de los teselados pentagonales muestra que aún hay sitio para los aficionados -y las aficionadas- en el olimpo de la investigación matemática
300
¿Cuántos fueron en realidad los 300 de Leónidas y qué propiedades posee este famoso número?
Fullerenos, balones y cúpulas geodésicas
¿En qué se parecen los balones de fútbol, las cúpulas geodésicas y ciertas macromoléculas formadas por átomos de carbono?
Números poligonales centrados
¿Podemos saber cuántas flechas hay en un carcaj contando solo las de la parte exterior del haz?
Pentágonos y hexágonos
¿Cuántos pentágonos y hexágonos conforman la superficie de un balón de fútbol?
Números figurados
Diofanto, Nicómaco y otros grandes matemáticos de la antigüedad estudiaron los números figurados
Números triangulares y cuadrados
La consabida colocación de los bolos en el ‘bowling’ configura un número triangular
Problemas librescos
Hay libros de problemas y problemas de libros, problemas librescos y libros problemáticos…
Lotería y matemáticas
¿Pueden las matemáticas aumentar nuestras probabilidades de ganar un premio de la lotería?
Indultos problemáticos
Los problemas lógicos de prisioneros que pueden -o no- ser indultados son tan numerosos como interesantes
Viajes de ida y vuelta
¿Cuánto tiempo te quedarías voluntariamente en el inhóspito planeta Venus?
Los siete mensajeros
¿Cuánto tardan los mensajeros en sus viajes de ida y vuelta entre el campamento móvil y la capital del reino?
Naipes y balas
¿Cuál es la probabilidad de derribar de un tiro a un indio que huye a caballo?
Pájaros, peces y balanzas
¿Qué ocurre en una balanza cuando el contenido de sus platillos tiene vida propia?
La moneda más pesada
Identificar la falsa moneda en medio de las auténticas requiere a veces no poco ingenio
Smullyan, el infinito y algo más
En su libro ‘Satán, Cantor y el infinito', el matemático nos ofrece una fascinante retahíla de preguntas desconcertantes y respuestas sorprendentes
Acertijos cocinados
El “cocinado” de acertijos era uno de los atractivos de la sección de juegos matemáticos del maestro Martin Gardner
La paradoja de Cantor
El propio padre de la teoría de conjuntos se dio cuenta de las paradojas derivadas de una concepción ingenua
El programa de Hilbert
El científico se propuso dotar a las matemáticas de un conjunto de axiomas completo y libre de paradojas
La máquina de Turing
La hormiga de Langton, de la que nos hemos ocupado en semanas anteriores, es también una máquina de Turing
Autómatas celulares
Sin más materiales que una hoja de papel cuadriculado, un lápiz y una goma, podemos crear un autómata celular
La hormiga de Langton
Menos conocida que el juego de la vida de Conway, la hormiga de Langton es un “autómata celular” igualmente fascinante
Policubos
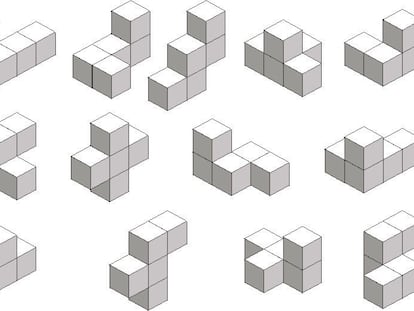
Aumentando el grosor de un poliominó hasta hacerlo igual al lado de los cuadrados obtenemos un policubo
Poliformas
Los poliominós son un caso particular de una familia de figuras más amplia en la que el elemento repetido puede ser cualquier polígono
Poliominós
Los poliominós generalizan el concepto de dominó a un número cualquiera de cuadrados adyacentes
Pentominós
Añadiendo un cuadrado a cada tetrominó de todas las formas posibles obtenemos los 12 pentominós
Tetrominós
El popular videojuego Tetris se basa en los tetrominós, ampliación del concepto de dominó a cuatro cuadrados adyacentes
Trominós
El concepto de dominó -dos cuadrados iguales unidos por un lado común- puede generalizarse a tres o más cuadrados
Mira y di
En sus ‘Brotes’ y su secuencia ‘look-and-say’, Conway aunó la investigación matemática más rigurosa con el juego y el humor
El jugador magistral
‘Sprouts’ (brotes), el también conocido como ‘Juego del drago’ de John Horton Conway
Tatamis
Los tatamis son esteras o colchonetas de 90 x 180 centímetros, como enormes fichas de dominó, usadas para recubrir suelos y tarimas
_
Últimas noticias
Los incendiarios provocan 20 fuegos nocturnos en Cantabria, con seis aún activos, aprovechando el viento del sur
Un hombre es apuñalado en el pecho durante una pelea en Toledo
La noche más grande de Raphael: los Grammy Latinos le honran como Persona del Año en una gala llena de música y lágrimas
El Rey cierra su visita China con un acto de apoyo a las empresas españolas en el gigante asiático
Lo más visto
- Juicio al fiscal general del Estado, Álvaro García Ortiz - 12 de noviembre de 2025 | El fiscal general niega haber filtrado el correo y justifica el borrado de su móvil por seguridad
- EE UU retira de un cementerio militar de la II Guerra Mundial en Países Bajos una placa sobre la segregación racial en su ejército
- La defensa del fiscal general ataca “las inferencias” de la UCO y los agentes aseguran: “No hacemos investigaciones prospectivas”
- La Ertzaintza se convierte en la primera policía en informar sobre la procedencia de sus detenidos
- Jornada política del 12 de noviembre de 2025 | Sánchez llama a Junts a volver a la negociación: “Necesitamos sus votos, pero ustedes también los nuestros”
newsletter
Recibe la mejor información en tu bandeja de entrada
_