La teoría de Ramsey

Vamos a hacer una pausa en nuestro periplo por el Sistema Solar en busca de agua y de vida para detenernos brevemente en el problema planteado la semana pasada.

Recordemos el problema en versión resumida: Dadas diez personas tales que en cualquier grupo de tres de ellas hay al menos dos que no se conocen, demostrar que hay al menos un grupo de cuatro personas en el que ninguna conoce a otra.

La discusión entre nuestros "usuarios destacados” Manuel Amorós y Francisco Montesinos (ver comentarios de la semana pasada) desemboca en una pista: para resolver el problema, puede ser útil abordar antes este otro:

"Demostrar que, en un grupo de seis personas, o bien hay al menos tres que se conocen entre sí, o bien hay al menos tres que no se conocen entre sí".

Este tipo de problemas remiten a la denominada “teoría de Ramsey” (en honor del matemático y filósofo británico Frank P. Ramsey), que estudia las condiciones que se han de cumplir para que en un conjunto dado aparezca un cierto tipo de orden. O, más concretamente, cuántos elementos ha de haber en un conjunto para que aparezca una determinada propiedad.

El “principio del palomar” puede considerarse un caso sencillo de la teoría de Ramsey, ya que podemos enunciarlo así: ¿Cuántas palomas ha de haber para que, dado un conjunto de n palomares, haya al menos un palomar con más de una paloma? La respuesta, en este caso, es obvia: ha de haber más palomas que palomares; es decir, si llamamos m al número de palomas, la condición pedida es m > n. Un ejemplo menos sencillo podría ser un acertijo misantrópico planteado hace unos meses en estas mismas páginas: Si el 70% de los hombres son feos, el 70% son tontos y el 70% son malos, ¿cuál será, como mínimo, el porcentaje de hombres que reúnan las tres “cualidades”, es decir, que sean a la vez feos, tontos y malos?

El teorema de la amistad

El problema de las seis personas antes enunciado es, en realidad, todo un teorema, conocido como “teorema de la amistad”, y también como “teorema de amigos y desconocidos”.

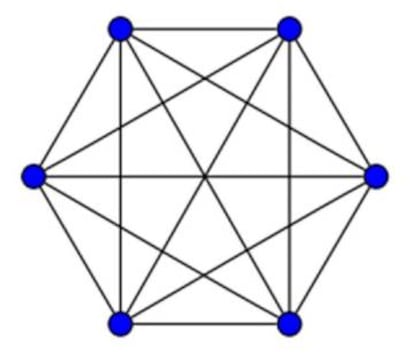
Un grupo de seis personas en el que cada una se relaciona de alguna manera con cada una de las demás, se puede representar esquemáticamente mediante un hexágono con todas sus diagonales. En teoría de grafos, es un grafo completo, pues cada nodo (cada vértice del hexágono) está unido a todos los demás. Pues bien, si las personas que se conocen las unimos con un trazo rojo y las que no se conocen con un trazo azul, el teorema de la amistad demuestra que habrá al menos un triángulo rojo o un triángulo azul (es decir, un grupo de tres conocidos o un grupo de tres desconocidos). ¿Cómo se demuestra? Y si hubiera solo cinco personas, ¿podríamos afirmar lo mismo?

El “problema del final feliz”, denominado así por Paul Erdös (por razones extramatemáticas), está estrechamente relacionado con la teoría de Ramsey, y dice así:

Cualquier conjunto de cinco puntos en el plano en posición general (sin que haya tres o más en línea recta) tiene un subconjunto de cuatro puntos que son los vértices de un cuadrilátero convexo.

Pero ese es otro artículo.

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos Maldita física, Malditas matemáticas o El gran juego. Fue guionista de La bola de cristal.