Poliformas

Además del oscilador R, equivalente al pentominó F, nos preguntábamos la semana pasada qué otros patrones típicos del juego de la vida se corresponden con poliominós. Tal vez el caso más claro sea el tetrominó O, que en el juego de la vida es una “vida estática” (¿por qué se denomina así?).

Como era de prever, el número de poliominós crece rápidamente al aumentar el número de cuadrados. Hay 1 dominó, 2 trominós, 5 tetrominós, 12 pentominós, 35 hexominós, 108 heptominós y 369 octominós, y la secuencia sigue creciendo a un ritmo irregular pero próximo al de una progresión geométrica de razón 3:

1, 2, 5, 12, 35, 108, 369, 1.285, 4.655, 17.073, 63.600…

Los 35 hexominós suman un total de 210 cuadrados, por lo que, en principio, se podría formar con ellos un rectángulo de 14 x 15, 10 x 21, 7 x 30, 6 x 35 o 5 x 42. Pero solo en principio, pues ninguna de estas construcciones es posible, como se puede ver aplicando el mismo criterio de paridad al que hemos recurrido en otros casos contemplados recientemente:

Efectivamente, si en cualquiera de los rectángulos anteriores coloreamos los cuadrados alternativamente de blanco y negro, como en un tablero de ajedrez, tendremos, obviamente, el mismo número de casillas blancas y negras: 105 de cada. Pero si hacemos lo mismo con los hexominós, vemos que en 11 de ellos hay un número par de cuadrados de cada color (2 blancos y 4 negros o viceversa) y en 14 de ellos hay un número impar de cada color (3 blancos y 3 negros); por lo tanto, los hexominós sumarán, en total, un número par de cuadrados blancos y un número par de negros, por lo que no podrán formar un rectángulo en el que ha de haber 105 de cada color.

Sí que es posible, sin embargo, componer elegantes rectángulos y cuadrados “agujereados” como el de la figura.

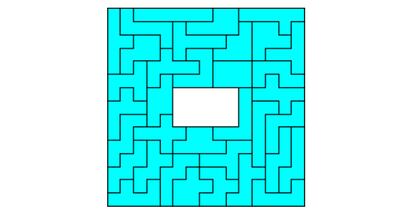
De los 35 hexominós, 11 son desarrollos planos del cubo. Mis sagaces lectoras/es pueden entretenerse doblándolos mentalmente.

Como vimos, hay un solo heptominó con agujero, a partir del cual podemos obtener 6 octominós con agujero distintos. El más obvio y regular es la cuadrícula de 3 x 3 sin el cuadrado central.

Polidiamantes y otras poliformas

Generalizando el concepto de dominó a un número cualquiera de cuadrados adyacentes, se obtienen los poliominós: trominós, tetrominós, pentominós… Pero, a su vez, el concepto de poliominó se puede ampliar a todo tipo de polígonos.

Especial interés revisten las poliformas de polígonos regulares. Además de los poliominós, cuya “célula”, como hemos visto es el cuadrado, las más destacadas son los polidiamantes (llamados así porque dos triángulos equiláteros que comparten un lado forman el consabido “diamante” de la baraja inglesa) y los polihex, integrados, respectivamente, por triángulos equiláteros y hexágonos regulares, que comparten con el cuadrado una singular propiedad en lo que a la acumulación “polifórmica” se refiere (¿cuál es esa propiedad que solo estos tres polígonos regulares poseen?).

La versatilidad de los triángulos equiláteros es menor, obviamente, que la de los cuadrados; solo hay 1 tridiamante y 3 tetradiamante. ¿Cuántos pentadiamantes hay? ¿Y hexadiamantes?

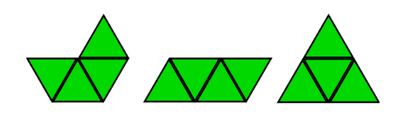
Invito a mis sagaces lectoras/es a explorar el inagotable mundo de las poliformas en busca de secuencias y singularidades.

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aquí a nuestra newsletter