El juego de la vida
Una cuadrícula con algunas casillas coloreadas y unas reglas sencillas ejemplifican la autoorganización de la vida
La constante de Conway, a la que está dedicado el artículo anterior, es el valor al que tiende la razón entre los respectivos números de cifras de dos términos consecutivos de la secuencia Look-and-Say. Si observamos los primeros términos de la secuencia: 1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, 31131211131221…, vemos que los respectivos números de cifras de cada término forman a su vez la secuencia 1, 2, 2, 4, 6, 6, 8, 10, 14…, y si dividimos cada término por el anterior obtenemos 2, 1, 2, 1.5, 1, 1.333, 1.25, 1.4…, y esta última secuencia, como demostró Conway, tiende a un número irracional algebraico: 1.30357…, que es la única solución real y positiva de una ecuación de grado 71.
Y lo más sorprendente es que se llega a este valor (de ahí su categoría de “constante”) independientemente de cuál sea el número inicial de la secuencia Look-and-Say, con excepción del 22, que da lugar a una repetición infinita de sí mismo, puesto que su descripción es “dos doses”.
El juego de Conway
Pero el prolífico matemático británico John Conway, que a sus ochenta años sigue en plena forma, es conocido sobre todo por su “juego de la vida”, popularizado en los años setenta del siglo pasado por Martin Gardner en su famosa sección de juegos matemáticos de Scientific American, y que durante un par de décadas se convirtió en un auténtico objeto de culto entre matemáticos y programadores.
En una cuadrícula ilimitada, cada casilla es una célula que puede estar “viva” o “muerta” (coloreada o en blanco, encendida o apagada, con una ficha en ella o vacía…). Dado un grupo inicial de células vivas, su configuración evoluciona de acuerdo con las siguientes reglas:
-Una célula viva muere (por aislamiento) si en su entorno hay menos de dos células vivas, o (por superpoblación) si hay más de tres.
-Una célula viva sigue viva si en su entorno hay dos o tres células vivas.
-Una célula muerta revive si en su entorno hay tres y solo tres células vivas.
El entorno de una célula lo constituyen las ocho células que la rodean y con las que, por tanto, está en contacto, aunque solo sea por un vértice.
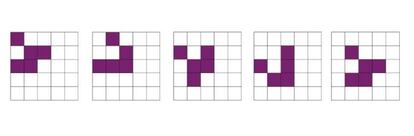
En la figura vemos una configuración de cinco células vivas que se autorreproduce en cuatro pasos, y en el proceso se desplaza diagonalmente una casilla hacia la derecha y hacia abajo. Invito a mis sagaces lectoras/es a buscar otros patrones autorreproductores (denominados “osciladores” en la terminología del juego de la vida), o dotados de otras propiedades interesantes.
Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos Maldita física, Malditas matemáticas o El gran juego. Fue guionista de La bola de cristal.
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.
Sobre la firma
