El triángulo de Pascal

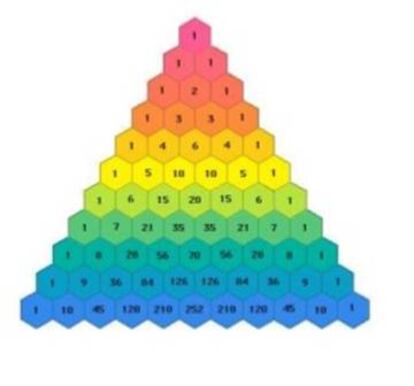
Nos preguntábamos la semana pasada si se puede establecer alguna relación entre el triángulo de Sierpinski y el triángulo de Pascal. Como ha señalado Guillermo Navas, coloreando los números impares del triángulo de Pascal y dejando en blanco los pares, se obtiene un triángulo de Sierpinski (ver comentario 144 de la entrega anterior).

En cuanto a la superficie (S) del copo de nieve de Koch, es fácil ver que, si tomamos como unidad el área del triángulo inicial, las sucesivas adiciones de áreas dan lugar a la serie siguiente:

S = 1 + 1/3 + 2²/3³ + 2⁴/3⁵ + 2⁶/3⁷…

Podemos hallar S mediante un sencillo y elegante “truco”, restando 1 a ambos miembros de la igualdad y luego multiplicándolos por 4/9:

Más información

Números normales

Piensa un número

4/9 (S – 1) = 2²/3³ + 2⁴/3⁵ + 2⁶/3⁷ + 2⁸/3⁹… = S – 1 – 1/3

4S – 4 = 9S – 9 – 3

5S = 8

S = 8/5 = 1,6

El perímetro del copo, sin embargo, crece indefinidamente, puesto que se trata de una progresión geométrica creciente: en cada paso, cada lado de la configuración anterior se multiplica por 4/3. Nos encontramos, pues, con una sorprendente figura de área finita y perímetro infinito.

El triángulo del tartamudo

Hemos visto la relación del triángulo de Sierpinski con el de Pascal. Recordemos la sencilla construcción de este último: en su primera fila hay un único 1, en la segunda dos 1, en la tercera dos 1 con un 2 entre ellos… En cada fila, cada número es la suma de los que tiene justo encima (solo uno -un 1- en el caso de los extremos y dos en el de los demás). Estos números son los coeficientes del desarrollo de las sucesivas potencias de una suma de dos sumandos: (a + b)ⁿ, o sea, del binomio de Newton:

(a + b)⁰ = 1

(a + b)¹ = 1a + 1b

(a + b)² = 1a² + 2ab + 1b²

(a + b)³ = 1a³ + 3a²b + 3ab² + b³

El triángulo de Pascal se conoce también como triángulo de Tartaglia, en honor del matemático italiano Niccolò Fontana, apodado Tartaglia por su tartamudez, que lo estudió antes que Pascal, aunque menos a fondo. Pero en realidad tampoco fue él el primero, pues en India se conocía este triángulo numérico desde al menos el siglo X, y en Persia lo estudió, entre otros, el gran matemático y poeta Omar Jayam.

La sencilla configuración de este triángulo numérico encierra interesantes propiedades. Podemos relacionarlo con las potencias de 2, con la sucesión de Fibonacci e incluso con los escurridizos números primos. ¿De qué maneras? ¿Qué otras propiedades y posibles generalizaciones ves en él, sagaz lector(a)?

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos Maldita física, Malditas matemáticas o El gran juego. Fue guionista de La bola de cristal.