

Marcelinho se sale en Liubliana
El Barça exhibe su enorme superioridad ante un rival menor
Recomanem...
48H Open BCN; Yelle; Ester Formosa Quartet; Le Nuvole.

"La pesadilla se acaba"
Els aires de la plaça Tahrir arriben a Barcelona
Riccardo Muti seduce con Cherubini (y con 'Asturias, patria querida')
El músico italiano, que pronunciará uno de los discursos de la ceremonia de entrega, dirige en Oviedo el 'Réquiem' de su compatriota
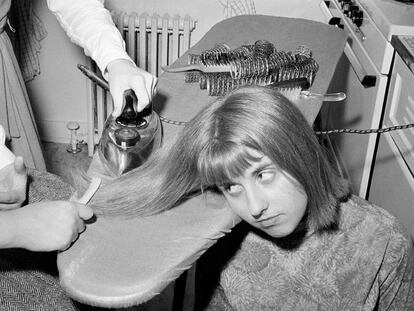
Guía definitiva para comprar unas planchas de pelo
Te ayudamos a elegir la plancha que mejor se adapta a la personalidad de tu cabello para sacarle el máximo partido.

"Hoy ha ganado la democracia"
Punto final a la pesadilla
La democracia española ha triunfado contra los fanáticos que, arrogándose una representación que los ciudadanos vascos jamás les concedieron, asesinaron a más de 800 personas. ETA ha anunciado que abandona la violencia, la pesadilla ha terminado.

El gasto social cae en 2012 cuatro veces más que el Presupuesto de la Xunta
Las consellerías de Educación, Sanidade y Benestar pierden 52 millones de euros

"Una gran noticia"
Rajoy destaca que no ha habido ninguna concesión política tras la decisión de ETA
El dividendo de la paz libia
Los beneficios de no tener que lidiar con la diplomacia de Gadafi son incalculables para el sistema mundial
"L'Odissea' és aventura i manual d'ètica"
Veronese, Marthaler i sargantanes
Agenda
Concerts

“Es un día grande para la libertad en España”

Lytro, la cámara bonita que lo enfoca todo
Está pensadas para internet y las redes sociales y permite que el espectador elija el punto más nítido de la imagen.
Gospel, el gust per l'energia vocal

"No sin memoria"
El presidente del Gobierno pide unidad y apoyo al nuevo Gobierno para gestionar el final de la banda terrorista
Francia se toma su tiempo para reaccionar a la noticia
Las ediciones digitales dan relieve al anuncio en sus primeras páginas Zapatero informó por teléfono a Sarkozy

Partículas en movimiento
Sofía Nieto, estudiante de doctorado en Matemáticas en la <a href="http://www.uam.es/ss/Satellite/es/home" target="_blank">Universidad Autónoma de Madrid</a>, presenta el 32º desafío con el que EL PAÍS celebra el <a href="http://www.rsme.es/centenario/" target="_blank">centenario de la Real Sociedad Matemática Española</a>. Envía tu respuesta antes de las 0.00 horas del martes 25 de octubre (medianoche del lunes, hora peninsular española) a <a href="mailto:problemamatematicas@gmail.com" target="_blank">problemamatematicas@gmail.com</a>, entre los acertantes sortearemos una <a href="http://www.elpais.com/promociones/matematicas/" target="_blank">biblioteca matemática</a> como la que cada domingo se distribuye con EL PAÍS. <p>A continuación, para aclarar las dudas y en atención a nuestros lectores sordos, añadimos el <b>enunciado del problema por escrito</b>.</p> <p>Tenemos una caja con forma de prisma recto de altura 40 cm y base un triangulo equilátero de lado 60 cm. Introducimos en ella 5 partículas, que hay que pensar que son como puntos, que se mueven al azar por la caja.</p> <p>El desafío consiste en demostrar que, en cualquier momento que observemos las partículas dentro de la caja, habrá al menos dos partículas que disten entre sí estrictamente menos de 50 cm. </p> <p>(Guión de Eva Elduque Laburta, profesora del <a href="http://www.unizar.es/ttm/" target="_blank">Taller de Talento Matemático de Aragón</a>) </p><p><a href="http://www.elpais.com/articulo/sociedad/desafios/matematicos/elpepusoc/20110712elpepusoc_8/Tes" target="_blank">DESAFÍOS ANTERIORES Y SUS SOLUCIONES</a></p>

Euskadi se enfrenta al reto de asentar la convivencia
Las víctimas rechazan de entrada una convivencia fácil e inmediata con los asesinos
Los mayas perviven en su cocina
Unas jornadas gastronómicas en Barcelona acercan la riqueza de los sabores de la gastronomía de la antigua civilización mesoamericana

Gora Euskadi Askatuta (libre de ETA)

Gora Euskadi Askatuta (libre de ETA)
Gabilondo explica que, en el día en que ETA ha dejado las armas, todos somos conscientes de que estamos cerrando un capítulo definitivo. <p> <strong><a href="http://blogs.elpais.com/la-voz-de-inaki/">Videoblog La voz de Iñaki Gabilondo</a></strong> </p>
Hirvonen y Loeb se juegan el título en el Rally Catalunya
Los dos pilotos, empatados en el Mundial, disputarán la penúltima prueba del campeonato
"Para escribir una novela hay que corregir los errores del periodismo"
Gabriela Cañas aprovecha sus más de 30 años en EL PAÍS y el incendio del edificio Windsor para desarrollar su primera novela, 'Torres de fuego'