Bauzá confía en sacar su plan tras ver a la vicepresidenta
El presidente balear opta por el tono conciliador con Elena Salgado
Una única suma posible de cuadrados
Madrid|
Hay una sola combinación de cuatro cuadrados perfectos distintos de cero cuya suma sea 2^2012 y ninguna que dé como resultado 2^2011.- El ganador de una biblioteca matemática ha sido esta semana Iago Vaamonde Paniagua, de Vigo.- El viernes plantearemos cinco nuevos desafíos
Una única suma posible
|
Ya hay solución para el decimonoveno desafío matemático con el que EL PAÍS celebra el <a href="http://www.rsme.es/centenario/" target="blank">centenario de la Real Sociedad Matemática Española</a> y que planteó <a href="http://personal.us.es/meneses"> Juan González-Meneses</a>, Profesor Titular de la <a href="http://www.us.es/">Universidad de Sevilla</a>. Hay una manera de descomponer 2^2012 como suma de cuatro cuadrados, y ninguna manera de descomponer 2^2011. El ganador de <a href="http://www.elpais.com/promociones/matematicas/">una biblioteca matemática</a> como la que entrega cada semana EL PAÍS ha sido en esta ocasión <b>Iago Vaamonde Paniagua</b>, estudiante de Ingeniería Industrial, de Vigo. Este domingo, en el quiosco, por 9,95 euros con el periódico, <i>Hipotecas y ecuaciones. Las matemáticas de la economía</i>, de Lluís Artal y Josep Sales.<p><a href="http://www.elpais.com/articulo/sociedad/unica/suma/posible/elpepusoc/20110726elpepusoc_21/Tes">VER SOLUCIÓN POR ESCRITO</a> Y <a href="http://www.elpais.com/articulo/sociedad/desafios/matematicos/elpepusoc/20110712elpepusoc_8/Tes">PROBLEMAS ANTERIORES</a></p>
Matematicos_19_solucion
|
8.000 millones solo para cubrir déficit
La Generalita no contempla la idea de Rubalcaba de que en 2012 se destine ese dinero a Sanidad
Tres muertos en un tiroteo en la localidad almeriense de Palomares
|
El supuesto autor de los disparos, que el día anterior había discutido con las víctimas, se ha entregado a la Guardia Civil
La Generalitat valenciana autorizó créditos al 0% al consejo de la CAM
Los préstamos a consejeros requerían el visto bueno del Gobierno autonómico Buena parte de las operaciones se cerraron a tipos inferiores a los de mercado
El PP envía al Gobierno la pelota para resolver el déficit autonómico
Rajoy y sus barones piden más tiempo y más dinero este año para afrontar la crisis
8.000 millones solo para cubrir déficit
El Gobierno catalán tiene como objetivo evitar que la cantidad extra que aportará el Estado a las comunidades se destine exclusivamente a Sanidad
Joe Arroyo, el juerguista que se negaba a desaparecer
|
El cantante colombiano fue un exponente de la salsa
Salgado rechaza aplazar la deuda de 24.000 millones de las comunidades
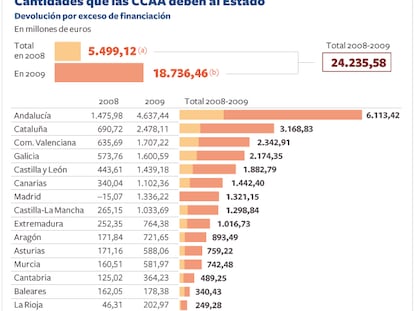
Elena Salgado rechaza aplazar la deuda de 24.000 millones de euros que deben las comunidades El Gobierno argumenta que ya aporta cada año desde la crisis más financiación autonómica El Ejecutivo anticipó 18.736 millones a las autonomías al pecar de optimista en los ingresos
Dimite otro congresista de EE UU por un escándalo sexual
|
El demócrata David Wu renuncia a su escaño tras admitir que mantuvo relaciones sexuales con una menor
Ernesto de Hannover, ingresado en Ibiza por una pancreatitis
Palma / Madrid|
El exmarido de la princesa Carolina de Mónaco sufrió esta dolencia hace cinco años
“Este es un problema de todas las autonomías”
La conselleira de Hacienda de la Xunta pedirá más tiempo para pagar lo que deben al Gobierno
Las deudas de las comunidades autónomas
|
El asesino es frío y siente que ha iniciado una cruzada, dice la defensa
|
Breivik dice estar sorprendido del éxito de su plan y de que la policía no le matara
"Buenas noches, ángel mío, duerme bien"
Londres|
El padre de Amy Winehouse se despide de la cantante fallecida.- Unas 200 personas, entre ellas Kelly Osbourne, acuden a los oficios fúnebres
De Camps a Fabra
|
El presidente de la Generalitat Valenciana anuncia un estilo distinto al de su antecesor
“La gente prefiere agrupar elecciones”
El candidato socialista cree que Zapatero y Griñán son los que tienen potestad para decidir
Un choque entre bandas en un penal de México acaba con 17 muertos
|
Degollada en Veracruz una periodista que cubría la información de sucesos
La Policía hace explotar un artefacto enterrado en el parque de Aluche
Madrid|
Un operario descubrió lo que parecía una granada de mano al cavar una zanja
El Barça mantiene el tipo en Múnich
|
El equipo azulgrana, plagado de jugadores del filial, se gana el pase a la final en la tanda de penaltis
Protección Civil levanta la alerta en la estación de trenes de Lleida por fuga de líquido inflamable
Lleida|
La circulación de tráfico ferroviario ha estado interrumpido durante casi dos horas
Plácido Domingo, embajador de la lucha contra la piratería
Londres|
El tenor español es nombrado presidente de la Federación internacional de la industria fonográfica
Una ley procesal para este mundo
Rubalcaba intenta diferenciarse de la agenda y el discurso del Gobierno
El candidato evita pronunciarse sobre el déficit autonómico y confrontar con el Partido Popular
Los vecinos de Castellbisbal llevan 12 días durmiendo en el CAP para que abra 24 horas
Castellbisbal (Barcelona)|
Los recortes médicos han dejado el Centro de Atención Primaria sin asistencia durante las noches y las tardes de los fines de semana