Problemas imposibles

La típica lámpara que se enciende y apaga desde dos interruptores (uno de los cuales es frecuente que falle, provocando un incómodo ir y venir de un interruptor a otro hasta conseguir encender la luz), mencionada la semana pasada, funciona de acuerdo con el esquema de la figura.

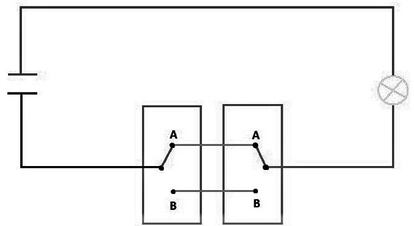
Cuando ambos interruptores hacen contacto en A, o ambos en B, se cierra el circuito y la lámpara se enciende; de lo contrario, se corta el circuito y la lámpara se apaga. (En el esquema parece todo muy sencillo; otra cosa es conectar los cables adecuadamente en una instalación real).

Nuestro asiduo comentarista Luca Tanganelli lleva la cuestión un paso más allá y pregunta cómo sería el circuito si una misma lámpara se encendiera y apagara desde tres interruptores. ¿Y si generalizamos el problema a una lámpara con n interruptores?

En cuanto a la bombilla de interruptor desconocido, esta es la solución de Vicente Pardo:

“Accionas el primer interruptor y esperas (pongamos tres minutos), lo apagas y accionas el siguiente y subes corriendo al primer piso. Tres posibilidades: la bombilla está encendida, lo cual confirma al segundo interruptor que acabas de accionar; si la bombilla está apagada te acercas y la tocas con la mano, si está caliente es el primer interruptor que accionaste durante tres minutos y si está fría se trata del tercer interruptor”.

Un consejo: si esperas tres minutos, no subas corriendo o, en el caso de que el bueno fuera el primer interruptor, te quemarías la mano.

De vuelta a la geometría

Tras unas cuantas semanas deambulando por la física y sus aledaños, y antes de que se solivianten los puristas que insisten en que esta es una sección de matemáticas, volvamos a la geometría con un par de problemas que parecen imposibles de resolver, uno por falta de datos y el otro por exceso.

El primero apareció en la maravillosa sección de matemática recreativa de Martin Gardner en Scientific American:

Dividir un triángulo obtusángulo en triángulos acutángulos o demostrar que es imposible.

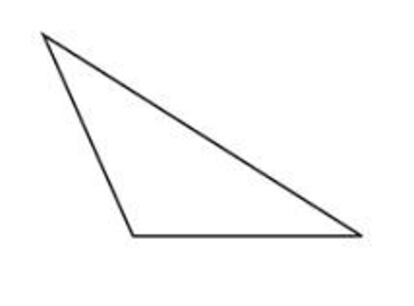
El segundo lo vi en uno de los muy recomendables libros de Clifford Pickover (no recuerdo en cuál; tal vez algún lector lo sepa) y aunque en su versión original tenía que ver con una astronave esférica y un alienígena con tentáculos, en resumen, dice así:

La superficie de una esfera y su volumen son ambos números enteros de cuatro cifras multiplicados por π. ¿Cuál es el radio de la esfera?

Y ya que tenemos una esfera a mano, imaginemos que está llena de un gas cuyas moléculas se agitan en su interior. ¿Existirá en todo momento un plano que corte la esfera de modo que haya el mismo número de moléculas a cada lado de este? (Se supone que el número de moléculas en el interior de la esfera es par, claro).

Por cierto,esta entrega de El juego de la ciencia se publica el 12 11 21. ¿Qué pueden decir mis sagaces lectoras/es del elegante palíndromo 121121?

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.