Las entrañas del capitán Grant
Las entrañas del capitán Grant
Las entrañas del capitán Grant

El Ayuntamiento cede su participación a cambio de 140 millones de ahorro

El duque de Palma, cobró del Gobierno y del Ayuntamiento de Valencia 3,7 millones de euros

La consejería hará una "convocatoria restringida voluntaria" para los centros

Aerocas estudia implantar una escuela de cetrería profesional aeroportuaria
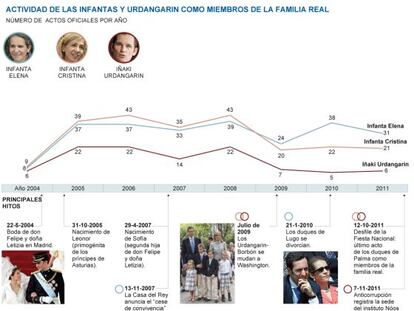
El último acto oficial de los duques de Palma fue el desfile de la Fiesta Nacional el 12 de octubre

Peligroso duelo dialéctico entre Washington y Moscú
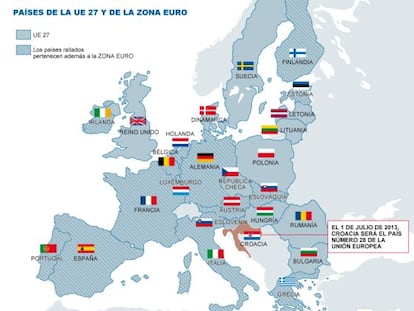
Unión fiscal y reforma del Tratado de Lisboa son algunos de los puntos clave de la reunión de los jefes de Estado y de Gobierno de la Unión Europea

El secretario general del PSdeG aspira a la reelección pese a los críticos en el seno del partido
La mujer tuvo que ser operada de urgencia y está fuera de peligro
Chan Koonchung; Helena Morén; Alexandra Maxeiner i Anke Kuhl.

Andreu Buenafuente rinde homenaje a Madrid en la nueva visita de su grupo de cómicos "a una ciudad en la que siempre hay algo nuevo que ver"

La secretaria de Estado norteamericana cifra en mil millones los internautas bajo gobiernos represivos
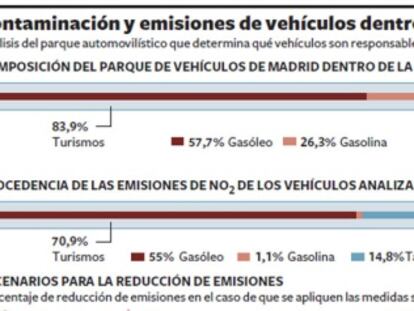
El objetivo es disuadir de aparcar dentro de la almendra central Será más caro en zonas con más demanda, cuando haya exceso de tráfico o mucha polución

Los mercadillos que ocupan en Navidad la mayor parte del centro apenas aportan dinero al Ayuntamiento
La red de laboratorios de investigación básica que dirige Hey financia a 100 universidades en el mundo

Los dirigentes de la Unión Europea intentan conciliar sus propios intereses con la defensa de la moneda única
El hallazgo, en un yacimiento arqueológico de Sudáfrica, muestra que los prehistóricos utilizaban plantas con efecto insecticida y quemaban periódicamente los jergones seguramente para desinfectarlos

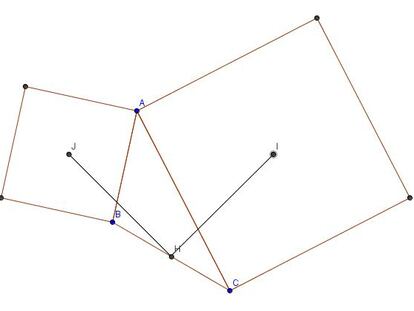
Miguel Ángel Morales Medina, licenciado en Matemáticas por la <a href="http://www.ugr.es/" target="blank">Universidad de Granada</a> y editor del <a href="http://www.rsme.es/content/blogcategory/36/90/" target="blank">Boletín de la RSME</a> propone y presenta el 39º y penúltimo desafío con el que celebramos el <a href="http://www.rsme.es/centenario/" target="blank">centenario de la Real Sociedad Matemática Española</a>. Manda tu solución antes de las 00.00 horas del martes 13 de diciembre (medianoche del lunes, hora peninsular española) al correo <a href="mailto:problemamatematicas@gmail.com">problemamatematicas@gmail.com</a> y participa en el sorteo entre los acertantes de <a href="http://www.elpais.com/promociones/matematicas/">una biblioteca matemática</a> como la que cada domingo distribuye EL PAÍS en el quiosco.<p></p><p> A continuación, para aclarar las dudas y <b>en atención a nuestros lectores sordos</b>, añadimos el enunciado del problema por escrito. </p><p> Partiendo de un triángulo cualquiera de vértices ABC, tomamos dos de sus lados, AB y AC por ejemplo, y dibujamos cuadrados apoyados en ellos. Llamamos I y J a los centros de los dos cuadrados y H al punto medio del lado del triángulo donde no hemos apoyado ningún cuadrado (el BC en este caso).</p><p> El desafío de esta semana consiste en demostrar que los segmentos HI y HJ tienen la misma longitud y que además forman un ángulo de 90º. La situación inicial puede verse <a href="http://www.elpais.com/fotografia/sociedad/Figura/39/desafio/matematico/elpfotsoc/20111208elpepusoc_21/Ies/">en esta figura</a>. </p><p> <a href="http://www.elpais.com/articulo/sociedad/desafios/matematicos/elpepusoc/20110712elpepusoc_8/Tes">DESAFÍOS ANTERIORES Y SUS SOLUCIONES</a></p>

Los intereses anuales de los créditos que faltan por pagar suben a 17 millones