La secuencia Look-and-say

Hablábamos la semana pasada sobre secuencias numéricas en ¿Cuál es el siguiente término? En ese artículo vimos ejemplos de secuencias numéricas interesantes y también una forma de continuar cualquier secuencia numérica que nos propongan, dando además la regla que justifica la elección que hagamos.

Más información

¿Cuál es el siguiente término?

Líneas con nombre

El problema de los besos de las esferas

También proponíamos dos secuencias para que los lectores las continuaran intentando adivinar la regla que se había usado para construirlas. La primera de ellas era la siguiente:

2, 10, 12, 16, 17, 18, 19,…

Como bien apuntaron Ozel Pociu e Ignacio Larrosa, el siguiente término de la sucesión sería el 200. De hecho, Ignacio dio algunos más:

2, 10, 12, 16, 17, 18, 19, 200, 201, 202, 203,…

La regla de construcción de esta secuencia es muy sencilla: escribir de menor a mayor los números que empiezan por la letra D al escribirlos en español. Como comentábamos en dicho artículo, es una secuencia muy conocida, pero no por ello deja de ser curiosa y apropiada para planteársela a compañeros y amigos para divertirse un rato pensando.

La segunda de las secuencias propuestas, que sirvió para finalizar el artículo, era la siguiente:

1, 11, 21, 1211, 111221, 312211,…

También Ozel Pociu e Ignacio Larrosa continuaron bien la secuencia con el término 13112221. La regla que se pedía encontrar para continuar esta secuencia es leer las cifras del número (agrupando las que sean iguales) y escribir lo que hemos leído también en forma de número.

Vamos a explicarlo un poco más despacio. Comenzamos con 1, y ahora leemos las cifras del número, agrupando las que sean iguales: “un uno”. Ahora, escribimos en forma de número lo que hemos leído: 11.

Hacemos lo mismo, leemos este número agrupando las cifras que sean iguales: “dos unos”. Y ahora escribimos lo que hemos leído: 21. Leemos de nuevo: “un dos, un uno”. Por tanto, el siguiente término es 1211. Y otra vez: “un uno, un dos, dos unos”, lo que nos dice que el término siguiente es el 111221. Y uno más: “tres unos, dos doses, un uno”, quedando ahora el 312211.

Haciendo lo mismo obtendríamos el siguiente término, que es el que pedíamos en el artículo anterior. Leemos: “un tres, un uno, dos doses, dos unos”, y nos queda el que comentábamos unos párrafos más arriba: 13112221. Sabiendo ya la regla podemos continuar la secuencia. Aquí la tenéis con unos cuantos términos más:

Esta secuencia es conocida con el nombre de secuencia Look-and-say (A005150 en la OEIS), y es bastante interesante no solo por la curiosa manera en la que está definida, sino por las propiedades que sabemos que cumple. Vamos a comentar algunas de ellas.

La primera es que la secuencia, tal cual la hemos descrito, cumple que sus términos van creciendo indefinidamente (pensad que podría ser que al agrupar los números consecutivos que sean iguales esto podría no ser así). De hecho, esto ocurre comencemos con el número que comencemos (hasta si es el cero), independientemente del número de cifras que tenga…excepto si es el 22. ¿Por qué? Muy sencillo, porque con el 22 obtenemos la siguiente secuencia:

22, 22, 22, 22, 22,…

Veamos otra curiosidad. Si os fijáis en los términos que os he dado en la imagen anterior, solo aparecen unos, doses y treses. Bien, pues el caso es que está demostrado que en ningún término de la sucesión aparecerá un número mayor que 3 a no ser que el inicial contenga a dicho número (o una cadena de más de tres números iguales consecutivos). Por ejemplo, si el inicial no tiene ningún 7 ni siete números iguales consecutivos, es imposible que aparezca un 7 en los términos posteriores.

Fijémonos ahora no en los términos, sino en la cantidad de cifras que tiene cada uno de ellos. Veamos qué ocurre si dividimos el número de cifras de cada uno entre el número de cifras del anterior:

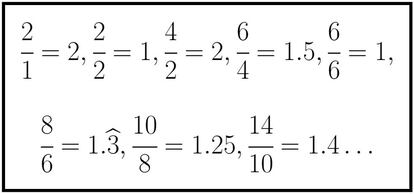
Bien, pues también está demostrado que dichas divisiones se van acercando al número 1’303577269034… Dicho número, que suele llamarse λ, es conocido como constante de Conway. De él se sabe que es irracional y que, sorprendentemente, es algebraico (¿qué pensáis que significa ese sorprendentemente?). Eso significa que es una de las soluciones de un cierto polinomio cuyos coeficientes son números enteros.

Pero además sabemos exactamente cuál es ese polinomio. Concretamente, es este monstruo de grado 71:

A la vista del mismo, ¿sabrías dar alguna razón que nos asegure que λ es irracional?

Todo lo que hemos comentado sobre la secuencia look-and-say lo sabemos gracias a los trabajos del gran matemático británico John Horton Conway. Según lo que sabemos, fue él quien estudió esta secuencia por primera vez y fue también él quien demostró todas las propiedades que hemos comentado y alguna más en The Weird and Wonderful Chemistry of Audioactive Decay.

Para finalizar, comentar que en dicho trabajo Conway también demuestra que todos los términos de la secuencia que comienza con 1 pueden descomponerse en grupos de subtérminos, los cuales forman una lista de exactamente 92 elementos. En A derivation of Conway’s Degree 71 “Look-and-say” Polynomial tenéis más información al respecto.

No podréis negarme que esta secuencia look-and-say está llena de curiosidad y de detalles que la hacen muy interesante. Y ahora os pregunto: ¿conocéis alguna secuencia extraña que tenga características de interés para hablar de ella aquí? Os agradeceremos que nos habléis de ellas en los comentarios.