¿Cuál es el centro de un triángulo?

Hace unas semanas hablábamos sobre el teorema de Napoleón, un bonito resultado sobre la geometría del triángulo que se asocia erróneamente al emperador francés. En él se habla de baricentro, punto que podría pasar por considerarse como el centro de un triángulo. Aunque esto tiene sentido, el baricentro no es el único punto al que tendría sentido llamar centro del triángulo. Hoy vamos a recordar cómo construir este baricentro y vamos a ver algunos otros puntos característicos de un triángulo que también podrían tener ese calificativo de centro del mismo.

Una mediana de un triángulo es un segmento que une un vértice con el punto medio del lado opuesto. Por tanto, un triángulo cualquiera tiene tres medianas. Bien, pues se da la circunstancia de que esas tres medianas se cortan en un único punto, que se denomina baricentro del triángulo. Aquí tenéis una imagen de esta construcción:

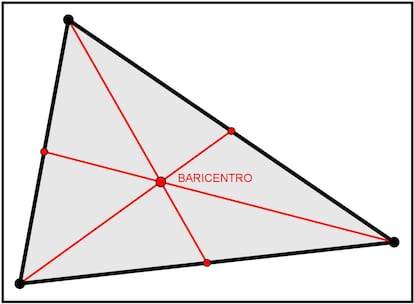
Cierto es que, al menos desde mi punto de vista, este baricentro es el punto que con más razón podría llevar el título de centro del triángulo, pero no es el único, ni mucho menos. Veamos algunos de los más destacados.

La bisectriz de un ángulo es la línea que divide dicho ángulo en dos ángulos iguales. Podríamos entonces trazar las bisectrices de los tres ángulos del triángulo y ver qué pasa. Si lo hacemos, vemos que las tres bisectrices se cortan también en un único punto, que se denomina incentro del triángulo. En la siguiente imagen podéis verlo:

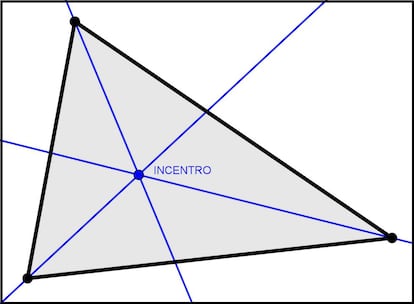
Su nombre se debe a que es el centro de la circunferencia inscrita al triángulo.

La mediatriz de un segmento es la recta perpendicular a dicho segmento que pasa por el punto medio del mismo. ¿Qué ocurre si trazamos las mediatrices de los tres lados del triángulo? Pues que, como en los casos anteriores, las tres se cortan en un único punto, que en este caso se denomina circuncentro del triángulo. Lo podéis ver a continuación:

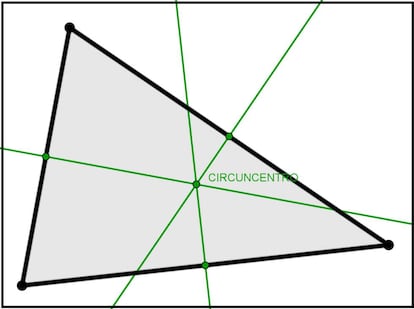
De manera parecida al caso anterior, el nombre de este punto se debe a que es el centro de la circunferencia circunscrita al triángulo.

Y veamos uno más. Una altura de un triángulo es el segmento trazado de manera perpendicular que va desde un vértice hasta el lado opuesto al mismo (bueno, en realidad va desde un vértice hasta la recta que contiene al lado opuesto, ya que en ciertos triángulos alguna de las alturas podría no llegar al lado opuesto en sí). Si las trazamos vemos que, de nuevo, las tres alturas de un triángulo se cortan en un único punto, que se denomina ortocentro del triángulo. Podéis verlo aquí:

¿Los queréis ver todos juntos? Pues, en el siguiente applet de GeoGebra, podéis contemplarlos por separado o todos a la vez (marcando o desmarcando las casillas correspondientes que tenéis a la derecha), y también podéis mover los vértices del triángulo y confirmar así que los tríos de segmentos o rectas descritos anteriormente se cortan siempre en un único punto, sea cual sea el triángulo de partida:

Y hay muchos más, y cuando digo muchos os aseguro que de verdad son muchos. En la web Encyclopedia of Triangle Centers, Clark Kimberling va recopilando todos los que se van encontrando y que tienen cierto interés.

Hasta el pasado 27 de julio, la web cuenta con más de 14000 “centros del triángulo”. Es cierto que algunos (quizá bastantes) son un poco “forzados”, pero no deja de ser curioso que haya tantas formas de definir puntos asociados a un triángulo que, de una forma y otra, puedan considerarse “centros” del mismo.

Como ya hemos comentado por aquí (ya sabéis que me encantan), una figura tan aparentemente simple como el triángulo esconde muchas curiosidades, algunas de ellas auténticas maravillas. Por eso, seguiremos (más pronto que tarde) hablando de ellos en este blog y mostrando todas esas características que hacen que el triángulo sea uno de esos objetos matemáticos que no te cansas de admirar.