Dirigentes y teoremas
¿Conocéis algún dirigente relacionado con un resultado matemático? Hoy os hablamos de dos de ellos

Hasta donde yo sé, no es muy habitual encontrar dirigentes políticos que tengan gusto reconocido por las matemáticas, y mucho menos que hayan realizado alguna aportación interesante dentro de este campo. Pero haberlos, haylos, y en los próximos párrafos vamos a hablar de dos de ellos y de las matemáticas que se les atribuyen.
El primero es todo un emperador: Napoleón Bonaparte. Es conocido el gusto de Napoleón por las matemáticas y su amistad con matemáticos muy importantes de su época, como Pierre Simon de Laplace, Joseph-Louis Lagrange y Lorenzo Mascheroni (quedaos con este nombre). Lo que puede que no sea tan conocido es que Napoleón da nombre a un teorema matemático relacionado con la geometría del triángulo.
El conocido como teorema de Napoleón es un bonito resultado sobre triángulos que os enuncio a continuación:
Dado un triángulo cualquiera, dibujemos triángulos equiláteros apoyados en sus tres lados. Entonces, el triángulo que tiene como vértices a sus baricentros también es equilátero.
Este teorema se cumple tanto si tomamos los triángulos “exteriores” a los lados del triángulo inicial como si tomamos los triángulos “interiores”. Y tiene además un interesante añadido: la diferencia entre el área del triángulo formado por los “vértices exteriores” y el área del formado por los “vértices interiores” es igual al área del triángulo inicial. Y todo esto es independiente del triángulo que tomemos inicialmente, se cumple sea cual sea dicho triángulo. En el applet de GeoGebra que tenéis a continuación (que tengo colgado en mi perfil de GeoGebraTube) podéis ver todo esto (moviendo los vértices podéis generar distintos triángulos y ver que el resultado se sigue cumpliendo):
Si os digo la verdad, sería magnífico que este teorema hubiese sido descubierto y demostrado realmente por Napoléon…pero en realidad esto no es así. Aunque la demostración del mismo no es demasiado complicada, los expertos coinciden en que Napoleón no tenía los conocimientos matemáticos necesarios para desarrollarla. Y la realidad parece ser que el teorema habría que atribuírselo a Lorenzo Mascheroni, amigo de Napoleón (como comentábamos antes) y gran geómetra. El hecho de que este teorema se haya acabado atribuyendo al emperador se debe a que Napoleón era un gran aficionado a los trabajos de Mascheroni, y ello le llevó a popularizar sus resultados. Tanto contribuyó a dicha popularización que este teorema ha acabado llevando (injustamente) su nombre.
Un bajón, ¿verdad? Habría estado bien que este consumado estratega militar también hubiese dedicado parte de su intelecto a demostrar un teorema matemático. Pero no, la historia nos ha arruinado una gran historia.
Tenemos que solucionar esto, no podemos acabar el artículo con este bajonazo. Y para ello os traigo nada menos que a un presidente de los Estados Unidos: James Garfield.
James Garfield fue el vigésimo presidente de los Estados Unidos, aunque por muy poco tiempo: fue elegido en marzo de 1881 y falleció en septiembre del mismo año a causa de las heridas provocadas por unos disparos que había recibido poco tiempo antes. En lo que se refiere a sus conocimientos, Garfield tenía una completa formación académica y además era matemático aficionado.
¿Y cuál es la relación de este presidente con las matemáticas? Pues muy sencillo: James Garfield desarrolló una demostración del teorema de Pitágoras, una de las muchas que se conocen, aunque esto no le resta ningún mérito.
Recordemos el enunciado del teorema de Pitágoras:
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Es decir, si h es la hipotenusa del triángulo rectángulo y a y b son los catetos del mismo, se cumple que a2+b2=h2.
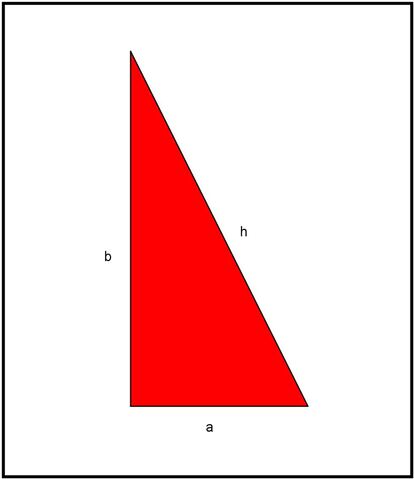
Vamos a ver la demostración de Garfield. Partimos de un triángulo rectángulo cualquiera, como el de la imagen:
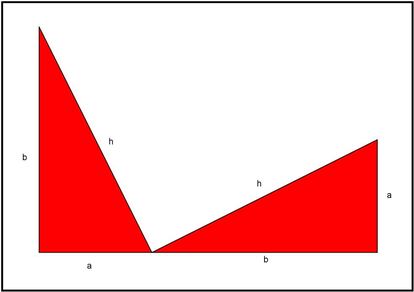
Copiamos el triángulo y los colocamos de manera que el cateto a de uno quede alineado con el cateto b del otro, y que queden pegados por los vértices asociados a los dos ángulos agudos. La cosa queda de la siguiente forma:
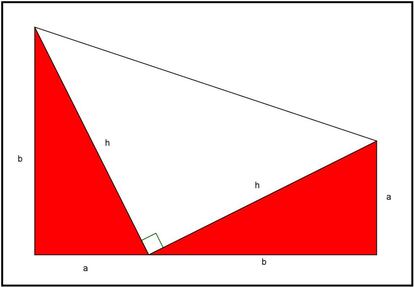
Como los ángulos agudos suman 900 y los catetos están alineados, el ángulo que queda en blanco también mide 900. Unimos ahora los vértices que quedan libres en los dos triángulos, quedan la figura como sigue:
Hemos construido un trapecio, que a su vez está dividido en tres triángulos rectángulos. Como sabemos calcular el área de un trapecio y también el área de un triángulo, vamos a calcular el área de la figura completa de dos formas, como trapecio y como unión de tres triángulos, y después las igualaremos. Aquí tenéis los cálculos:
Como trapecio:
El área de un trapecio es igual al producto de la suma de las bases, a y b en este caso (el lado de la izquierda y el de la derecha) multiplicada por la altura, a+b en nuestro trapecio, y dividido todo entre dos. Queda lo siguiente después de desarrollar la expresión:
Como unión de tres triángulos rectángulos, sabiendo que el área de un triángulo es base por altura dividido todo entre 2:
Igualando las áreas y cancelando los términos iguales en ambos miembros nos queda lo siguiente:
Vamos, lo que dice el teorema de Pitágoras. Bonita demostración, ¿verdad?
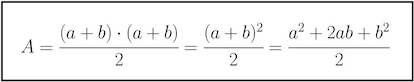
Para finalizar, os pido que si conocéis algún caso más de dirigente (o persona famosa) que tenga una cierta relación con las matemáticas nos lo digáis en los comentarios. Seguro que con vuestra ayuda conseguimos una lista de nombres realmente interesante.
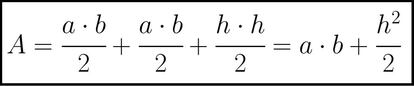
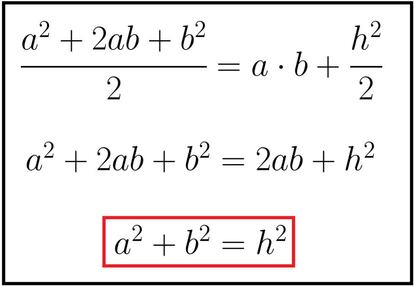
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































