Pitágoras y la demostración de los 200 TB

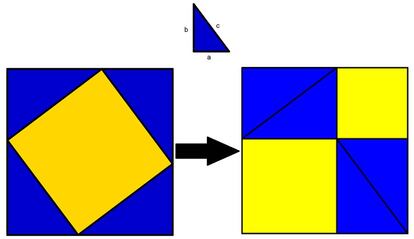
Creo que a estas alturas no es necesario presentar el famosísimo teorema de Pitágoras.Todos lo conocemos, todos lo hemos estudiado en nuestra época de colegio y podría asegurar que la gran mayoría nos acordamos de él. De todas formas, me vais a permitir que lo recuerde:

Teorema de Pitágoras: En un triángulo rectángulo cuyos catetos miden a y b y cuya hipotenusa mide c, se cumple que a²+b²=c².

Una lista de tres números enteros positivos (a, b, c) que cumplen el teorema de Pitágoras se suele llamar terna pitagórica.

Actualmente, se conocen multitud de demostraciones de este resultado, y las hay de diversos tipos: geométricas, algebraicas, que usan el cálculo... Teniendo en cuenta que con una demostración nos serviría para saber que el teorema es cierto, que se hayan desarrollado tantas (se conocen unas 400) habla muy bien del interés que ha suscitado el teorema de Pitágoras entre los matemáticos de todas las épocas (en esta web podéis ver un buen puñado de demostraciones). ¡¡Hasta un presidente de los Estados Unidos, James Garfield, encontró una!!

Se suele asignar a Pitágoras el honor de ser quien descubrió este teorema, hace unos 2500 años, aunque hay cierta controversia al respecto. Algunos historiadores de las matemáticas sostienen que ya lo conocían en Babilonia más de 1000 años antes que Pitágoras, también hay alguna prueba de su conocimiento en Mesopotamia más o menos por aquella época y otros aseguran que en India o en China se descubrió de manera independiente más o menos en la época del propio Pitágoras.

Pero no nos vamos a extender en la historia de este teorema, sino que vamos a volver a las ternas pitagóricas para hablar de un problema relacionado con ellas cuyo planteamiento es relativamente reciente y cuya solución se ha encontrado hace bien poco.

En la década de los 80 del pasado siglo XX, el matemático estadounidense Ronald Graham planteo el siguiente problema:

¿Se pueden colorear los números enteros positivos con dos colores, rojo y azul, de manera que no haya ninguna terna pitagórica (a, b, c) cuyos tres elementos tengan el mismo color?

Es decir, Graham preguntaba si se podían separar los enteros positivos en dos conjuntos disjuntos (sin elementos en común) de forma que ninguno de los dos conjuntos contuviera una terna pitagórica.

El problema, que se conoce como problema de las ternas pitagóricas booleanas, ha permanecido sin solución hasta este mismo año 2016. En mayo de este año, los matemáticos Marijn Heule (Universidad de Texas en Austin), Oliver Kullmann (Universidad de Swansea) y Victor Marek (Universidad de Kentucky en Lexington) han demostrado que la respuesta a dicho problema es NO. Más concretamente, lo que han demostrado es que hay muchas maneras de colorear los enteros positivos hasta 7824 con las condiciones indicadas antes, pero que al añadir el 7825 no existe ninguna forma de hacerlo.

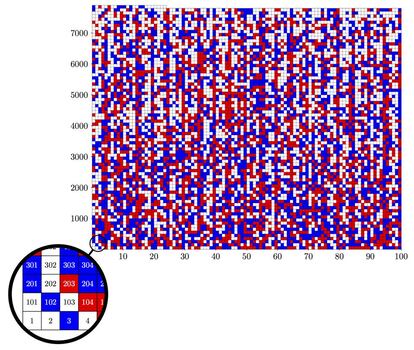
Pero, posiblemente, lo más llamativo del caso es la importancia que han tenido los ordenadores en esta prueba. Hay 2⁷⁸²⁵ formas de colorear los enteros positivos hasta 7825, número que es del orden de 10²³⁰⁰. Teniendo en cuenta que se estima que el número de partículas del universo es inferior a 10¹⁰⁰, creo que es fácil adivinar que comprobar una a una todas las posibles coloraciones es del todo imposible para el ser humano…

…e incluso para un ordenador. Un número como ése, un 1 seguido de 2300 ceros, es abismal. Por ello, nuestros protagonistas tuvieron que usar matemáticas para reducir drásticamente los casos a estudiar, dejándolos finalmente en una cantidad del orden del billón, 10¹². Sí, una cantidad que sigue fuera de nuestro alcance, pero que para un ordenador sí podría ser alcanzable.

Pero no para un ordenador cualquiera, sino para un superordenador. Ellos usaron Stampede, un superordenador de la Universidad de Texas, y tuvieron trabajando a sus 800 procesadores durante dos días, generando dicho trabajo un archivo de 200 Terabytes y, por tanto, convirtiendo a esta demostración en una de las más largas (si no la que más) de la historia de las matemáticas. Después, utilizando otro programa consiguieron comprobar que la solución era correcta. En el preprint que subieron a arXiv y en esta web de Marijn Heule tenéis más detalles sobre el desarrollo de la demostración.

Y por si alguien se pregunta qué ocurriría con más colores, se estima que la situación sería parecida. Por ejemplo, se cree que si se utilizan tres colores, también se encontraría un número, tipo el 7825 del caso anterior, para el cual no se podría colorear el conjunto de enteros positivos resultante con esos tres colores de manera que no hubiera ternas pitagóricas monocromáticas. En general, se piensa que para cualquier número finito de colores pasaría lo mismo, pero no está demostrado. Y dudo mucho que se pueda demostrar a corto plazo, aun con la ayuda de superordenadores, ya que si para dos colores se ha generado tal cantidad de información, es razonable pensar que para más colores el volumen de datos, y por tanto el coste en recursos y tiempo, sería muchísimo mayor, posiblemente inasumible actualmente.

Como no podía ser de otra forma, esta manera de resolver el problema ha generado cierta controversia en los círculos matemáticos. Dejando aparte que el trabajo de Stampede no dice nada acerca de por qué la cosa cambia al llegar al 7825, de qué característica especial puede tener dicho número para que ocurra esto, lo controvertido es el propio hecho de aceptar como demostración “matemática” el trabajo realizado por este supercomputador. ¿Es una demostración del resultado? Sí. ¿Esto son matemáticas? Pues…depende de a quién le preguntes.

De todas formas, no es ni mucho menos el primer caso de resultado matemático en cuya resolución el ordenador es parte esencial. Uno de los primeros casos fue la demostración de Thomas Hales de la conjetura de Kepler en 1998, y otro de los más conocidos es la demostración del teorema de los cuatros colores por parte de Kenneth Appel y Wolfgang Haken a mediados de los 70.

Estos dos casos son muy famosos, por ser problemas clásicos que habían permanecido sin demostración muchísimo tiempo, pero ni son ni serán los únicos que utilizarán el ordenador como parte fundamental de su resolución. Y, por tanto, el “enfrentamiento” entre los partidarios y detractores de este tipo de pruebas continuará dentro de la comunidad matemática.

¿Qué pensáis vosotros sobre este tipo de demostraciones?