El problema de los besos de las esferas

El problema de los besos de las esferas es una cuestión que ha interesado a muchos matemáticos desde hace, al menos, unos 300 años. Y en el transcurso de su estudio ha quedado patente lo sencillo que es a veces estudiar un problema en ciertas dimensiones y lo complicado que es hacerlo en otras. Vamos a plantear el problema y a comentar todo lo que se conoce de su solución.

El problema, como ya hemos comentado, va de colocar esferas “besando” a otra esfera inicial. Entendemos “besar” como tocar en un punto a dicha esfera, y pedimos que las esferas que coloquemos se toquen entre ellas en, como mucho, un punto. Además, todas las esferas deben ser iguales (la inicial y las que coloquemos después).

En dimensión 1, una recta, una esfera es un intervalo. Partiendo por tanto de un intervalo inicial, ¿cuántas esferas (intervalos) podríamos colocar “besando” a la esfera (al intervalo) inicial?

Sin mucho pensar, creo que está claro que sólo podemos colocar dos esferas de este tipo (una a cada lado de la esfera del principio). La situación quedaría como sigue (la roja es la esfera inicial):

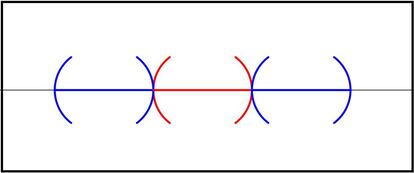
Al número de esferas que podemos colocar en cada situación se le denomina kissing number (en español podríamos llamarlo número de osculación). Entonces, en el caso de dimensión uno tenemos que el kissing number es 2.

Pasemos a dimensión dos, a un plano. En este caso, las esferas son las circunferencias de toda la vida. Colocamos, por tanto, una circunferencia, y después colocamos circunferencias iguales a ésta “besando” (tocando en un único punto) a la inicial y tocándose, como mucho, en un único punto entre ellas. ¿Cuántas podríamos colocar en este caso?

Es algo más complicado que el anterior, pero tampoco parece demasiado difícil concluir que en este caso son seis esferas las que podemos colocar “besando” a la inicial. La cosa quedaría tal que así (la inicial es la coloreada en rojo):

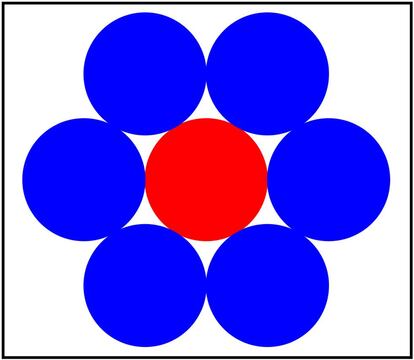
Por tanto, en dimensión dos el kissing number es 6.

Llegamos ahora al espacio. En este caso, en dimensión tres, una esfera es lo que todos entendemos cuando escuchamos la palabra esfera: una pelota. Hacemos lo mismo que antes: tenemos una esfera inicial (que, de nuevo, colorearemos de rojo) y colocamos esferas iguales que ellas “besando” a esta esfera inicial (de nuevo, estas esferas sólo pueden tocarse, como mucho, en un único punto). Antes de seguir leyendo, os invito a que penséis en ello: ¿cuántas esferas creéis que podréis colocar “besando” a la inicial?

En dimensiones uno y dos el problema es bastante sencillo, pero en dimensión tres la cosa comienza a complicarse. Si uno se mete en el problema, ve que no es demasiado complicado colocar 12 esferas “besando” a la inicial, pero seguro que aprecia que queda una nada despreciable cantidad de huecos entre ellas. Estos huecos invitan a pensar que, mediante una recolocación de estas 12 esferas, podríamos dejar espacio para colocar una más, con lo que tendríamos 13 esferas “besando” a la esfera inicial.

Newton y Gregory discutieron sobre si el kissing number en dimensión 3 era 12 ó 13. Su disputa no se resolvió hasta casi 300 años después

Este asunto fue objeto de disputa entre el gran Isaac Newton y el también matemático británico David Gregory a finales del siglo XVII. La cuestión le había surgido a Newton a raíz de unos estudios sobre mecánica celeste, y conjeturó que sería 12 las esferas que podríamos colocar. Sin embargo, David Gregory apoyaba la idea de que los huecos que dejan esas 12 esferas podrían dejar espacio para una más, con lo que serían por tanto 13 esferas.

¿Pensáis que serán 12 o, por el contrario, podremos colocar 13? Quizás algunos (o muchos) veáis que el problema tampoco es demasiado difícil, pero la realidad es que este paso a la tercera dimensión resultó mucho más complicado de lo que pueda parecer. Tanto es así que la cuestión no se resolvió hasta 1953, cuando Schütte y van der Waerden demostraron que el kissing number en dimensión 3 es 12, por lo que casi 300 años después Newton salía vencedor de la disputa contra Gregory (a finales del siglo XIX se presentaron algunas pruebas de este hecho, pero no eran totalmente correctas). En las siguientes imágenes podéis ver una posible disposición en la que las esferas que “besan” a la inicial (que, como antes, está coloreada en rojo) tienen sus centros en los vértices de un icosaedro regular cuyo centro es también el centro de la esfera inicial:

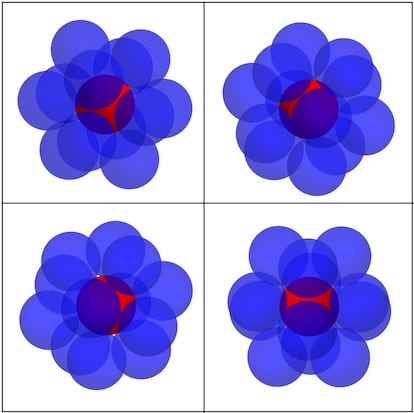
Si llamamos k(n) al kissing number en dimensión n, tenemos por ahora que k(1)=2, k(2)=6 y k(3)=12. Aunque para dimensiones superiores ya no tendremos imágenes descriptivas del problema (por razones evidentes), tiene mucho sentido preguntarse cómo es el kissing number para n mayor que 3. Bien, pues si ya en dimensión 3 la cosa era compleja, para dimensiones superiores aún más. De hecho, para n mayor que 3 sólo se conoce el kissing number para las dimensiones 4, 8 y 24. Concretamente, tenemos que k(4)=24, k(8)=240 y k(24)=196560. El caso n=4 lo resolvió Oleg Musin en 2003 en su trabajo The kissing number in four dimensions, y los casos n=8 y n=24 fueron resueltos por Henry Cohn y Abhinav Kumar en 2004. Podéis consultar Optimality and uniqueness of the Leech Lattice among lattices si estáis interesados en el tema.

Del resto de valores de n tenemos, como mucho, cotas del kissing number. Por poner algunos ejemplos, para n=5 sabemos que está entre 40 y 44; para n=6 se sabe que está entre 72 y 78; para n=7 se encuentra entre 126 y 134; y para n=9 entre 306 y 364. Veremos si en los próximos tiempos se concreta alguno de estos valores, estaremos atentos a ello. Mientras tanto, podéis leer más datos sobre el problema del kissing number en Kissing Numbers, Sphere Packings and Some Unexpected Proofs, de Florian Pfender y Günter M. Ziegler

Es curioso cómo un problema de enunciado tan sencillo puede ser tan fácil de resolver en algunos casos y tan complicado de demostrar en otros. Y no es, ni mucho menos, el único caso. Hay muchos otros problemas de enunciado simple y de sencilla exploración en casos pequeños que se complica enormemente cuando subimos de nivel. Hablaremos de otros casos en próximos artículos, pero sería interesante que propongáis los casos que conozcáis en los comentarios.