¿Cuál es el siguiente término?

Internet está repleto de páginas en las que nos proponen problemas relacionados con secuencias lógicas. Sabéis a qué me refiero, ¿verdad? Sí, esas secuencias en las que nos dan algunos términos y nos piden que, de manera lógica, “adivinemos” el siguiente.

Podemos encontrar problemas de secuencias lógicas de muchos tipos, como los relacionados con símbolos (nos dan una serie de símbolos colocados en distintas posiciones o coloreados de diferentes formas y nos piden que adivinemos el siguiente) o relojes (nos dan unos cuantos relojes con horas distintas y nos proponen que digamos cuál sería el que continúa la serie), pero los más comunes (y, posiblemente, los que dan más juego) son los problemas relacionados con secuencias numéricas.

Vamos a ver algún ejemplo. Imaginaos que os propongo que continuéis la siguiente secuencia numérica:

1, 2, 3, 4, 5,…

Posiblemente elegiríais como siguiente término al número 6. Sencillo, ¿verdad? Veamos otro ejemplo:

3, 5, 7,…

Aquí ya se nos podrían ocurrir más cosas sin necesidad de pensar demasiado. Podríamos imaginar que la secuencia corresponde con los números impares a partir del 3, por lo que el siguiente término sería el 9. Pero también tendría sentido que la secuencia fuera la que nos muestra los números primos impares, por lo que debería seguir con el número 11. Ambas respuestas serían correctas, y bastante razonables.

Y un ejemplo más. A ver quién puede seguir la siguiente secuencia:

2, 10, 12, 16, 17, 18, 19,...

¿Cuál sería el siguiente término? Os dejo que penséis y que nos contéis vuestros progresos en los comentarios (si alguien conocía la serie y, por tanto, ya sabía la respuesta que se espere un poco para comentarlo para dejar así que la gente piense).

Volvamos a la secuencia 3, 5, 7. Hemos dicho que tendría sentido seguirla con un 9 (números impares a partir del 3) o con el 11 (número primos impares). ¿Sólo con esos? ¿Se podría seguir con el número 14? ¿Tendría sentido que el siguiente término fuera el 47? ¿Y el 1111? Pues el caso es que sí, tendría sentido continuar esa secuencia con cualquier número que se nos ocurra, entendiendo “tener sentido” como que para cualquier número K podríamos encontrar una regla a partir de la cual obtenemos el 3, luego el 5, después el 7 y a continuación el número K elegido.

Esto está demostrado, y además desde hace ya tiempo. En 1795, Joseph Louis Lagrange publicaba un resultado que está muy relacionado con estas secuencias numéricas. Dicho resultado (que, por cierto, había sido descubierto por Edward Waring en 1779) dice básicamente que para cualquier secuencia de números podemos encontrar una regla (más concretamente, un polinomio) que para los valores 1, 2, 3, etc, nos da los términos de dicha secuencia.

Dicho polinomio, llamado polinomio interpolador, se calcula a partir de los términos de la propia secuencia. Podríamos entonces añadir el número que quisiéramos y después calcular el polinomio interpolador de la secuencia obtenida, obteniendo así la “regla” que explica el porqué de nuestra elección. No tiene por qué ser una regla sencilla, lo interesante es que la hay. Aquí os dejo las reglas que explicarían las elecciones 9, 11, 14, 47 y 1111 para la secuencia 3, 5, 7:

Alguno de vosotros pensaréis que con esto le acabamos de quitar toda la gracia a la búsqueda de reglas que expliquen una elección concreta del siguiente término de una secuencia numérica. Por ejemplo, para la secuencia

1, 2, 4, 8, 16,…

seguro que la mayoría (posiblemente todos) habríais contestado que el siguiente término es el 32, al ser la siguiente potencia de 2 (la secuencia propuesta es 2⁰, 2¹, 2², 2³, 2⁴). Pero con lo que hemos comentado antes ya sabemos que para cualquier número que eligiéramos podríamos encontrar una regla que le diera sentido.

Ahora, eso no significa que no podamos encontrar relaciones curiosas y bellas que expliquen ciertas elecciones “no habituales”. Por ejemplo, ¿y si os digo que busquéis alguna regla curiosa o interesante que explique que la elección del siguiente término de la secuencia fuera el 31?

Si, vale, elegimos el 31, calculamos el polinomio interpolador y ya tenemos la regla. Pero, en este caso, existe una bonita explicación para esta elección. Tomamos una circunferencia, elegimos puntos sobre ella y los unimos con segmentos de todas las formas posibles (cuidándonos de que no haya tres segmentos que se corten en un punto). Hemos esto, contamos el número de regiones en las que ha quedado dividido el círculo interior a dicha circunferencia.

Comenzamos tomando un punto nada más. En este caso no se puede trazar ningún segmento (necesitamos al menos dos puntos), por lo que nos queda una única región (el círculo completo). Tenemos entonces que el primer término de la secuencia es 1.

Tomemos ahora dos puntos. Ahora podemos trazar un único segmento, que divide al círculo en dos regiones. Entonces, el segundo término de la secuencia es 2.

Vamos ahora con tres puntos. Aquí podemos trazar tres segmentos, que dejan dividido el círculo en exactamente cuatro regiones. Por tanto, el tercer término de la secuencia es 4. En la siguiente imagen podéis ver estos tres primeros casos:

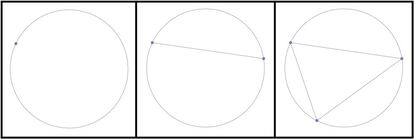
Con cuatro puntos se pueden trazar seis segmentos, que dividen el círculo en ocho regiones, y con cinco puntos podemos trazar diez segmentos, quedando el círculo dividido en dieciséis partes. Entonces, los siguientes términos de la secuencia son, efectivamente, 8 y 16. A continuación, podéis ver las dos situaciones:

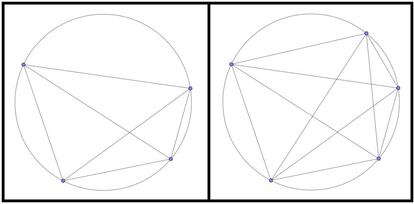
Y vayamos ahora al caso de seis puntos, el que corresponde al término que nos preguntaban. Unimos esos seis puntos de la forma comentada y contamos regiones. Podéis hacer vosotros mismos el dibujo, pero por si acaso no tenéis papel y boli a mano (bueno, o por si no tenéis muchas ganas de hacer dibujitos) os lo dejo yo hecho. Contad:

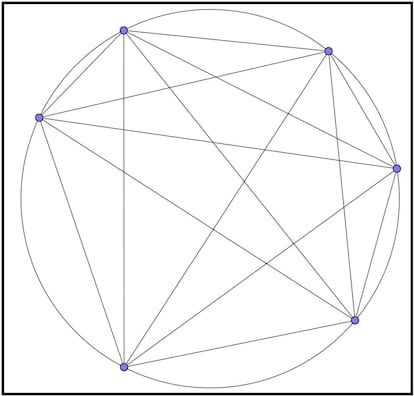
Exacto, el círculo interior queda dividido en 31 regiones exactamente. Tenemos entonces una secuencia que coincide con las potencias de 2 en los primeros cinco términos pero que difiere en el sexto. Y no sólo en este, sino que a partir de ahí las diferencias van siendo cada vez más grandes: 57 (frente a 64), 99 (frente a 128), etc. La regla (el polinomio) que nos calcula exactamente el número de regiones en las que queda dividido el círculo interior actuando de la forma descrita es la siguiente:

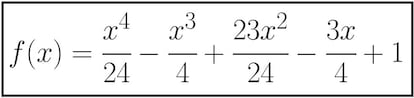
No creo que podáis negar lo curioso de este problema de las regiones y, por qué no decirlo, la belleza que contiene.

Muy interesante esto de las secuencias numéricas, un mundo en el que podemos encontrar todo tipo de situaciones curiosas y en el que nos podemos llevar muchas sorpresas. Para finalizar este artículo, os quiero proponer otra secuencia que, aunque es ciertamente conocida, no deja de tener interés. Es la siguiente:

1, 11, 21, 1211, 111221, 312211,…

Os invito a que penséis cuál sería el siguiente término de la serie, dando una regla que nos indique cómo encontrar los siguientes. Os pido, igual que antes, que si ya la conocéis no le fastidiéis el entretenimiento a quien quiera pensar. Dejad un rato para que la gente piense y, si pasa un tiempo y nadie lo dice, comentad la solución. Muchas gracias.