Los cubos de MacMahon

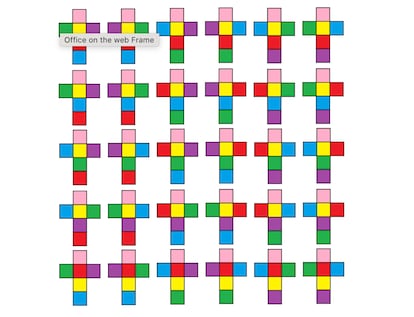
A pesar de que un lector llegó a la conclusión que los puzles de MacMahon propuestos la semana pasada son imposibles de resolver, en el caso del primero, el que involucra todas las piezas, hay 20 configuraciones posibles para el borde monocolor y nada menos que 13.328 soluciones distintas al rompecabezas. He aquí una de ellas:

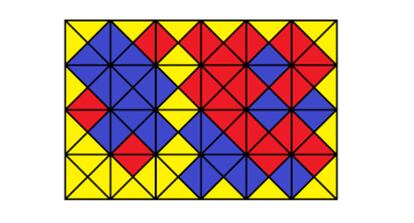
Obsérvese que la pieza monocolor amarilla está en una esquina. ¿Podría estar en otro lugar, en una configuración de perímetro amarillo?

Sin embargo, nuestro lector escéptico tendría razón si con las 24 piezas quisiéramos formar un rectángulo de 3x8 con los mismos requisitos; podemos disponerlos de forma que los lados en contacto sean siempre del mismo color, pero el perímetro no puede ser monocolor. ¿Por qué?

Con respecto a la posibilidad de plantear un juego tipo dominó con los cuadrados de MacMahon, dice Juan Zubieta:

“La idea de proponer un juego me parece muy atractiva. El hecho de que sean 24 piezas permite que el número de participantes sea 2, 3, 4 y se repartan la misma cantidad de cuadrados. La pega que le veo es que disponer de más colores enriquecería las posibilidades de diseñar un juego atractivo. Por ejemplo, se me ocurre esto: un jugador coloca una pieza y marca un triángulo de esa pieza con el que debe conectarse la siguiente; y así sucesivamente. Quien no tuviera el color elegido, debe pasar. Sería como un dominó limitado a un solo extremo que se extiende formando una línea libre. Posible regla adicional: siempre debe dejarse espacio para que la línea continúe sin cerrarse sobre sí misma”.

Y he aquí cómo calcula Salva Fuster (con la cuenta de la vieja avanzada) el número de posibles cubos distintos en blanco y negro:

“Me parece que el número de cubos en blanco y negro distintos que se obtiene es 10:

— Sin casillas blancas: 1.

— Con 1 casilla blanca: 1.

— Con 2 casillas blancas: 2 (o enfrentadas o contiguas).

— Con 3 casillas blancas: 2 (o comparten un vértice o forman una U).

— El resto de los casos es simétrico a los tres primeros si cambiamos las casillas blancas por las negras.

Por lo tanto, 1 + 1 + 2 + 2 + 2 + 1 + 1 = 10″.

Cubos multicolores

Y del cubo en blanco y negro pasemos al más colorido y preguntémonos de cuántas maneras distintas podemos colorear un cubo utilizando 6 colores, uno para cada cara. Este problema es equivalente al de averiguar de cuántas maneras distintas podemos situar en un dado los números del 1 al 6, y la respuesta es 30 (¿puedes demostrarlo?). Y estos dados multicolores son los cubos de MacMahon, que no se limitó a concebir sus puzles cromáticos en dos dimensiones, y con los que se pueden plantear un sinfín de interesantes retos. Por ejemplo:

—Forma con 8 de los 30 cubos uno de 2x2x2 “tipo Rubik reducido”, o sea, con una cara de cada color.

—Forma con 27 de los 30 cubos uno de 3x3x3 “tipo Rubik estándar”, o sea, con una cara de cada color.

—Elige uno de los 30 cubos y forma, con 8 de los restantes, un cubo de 2x2x2 semejante al elegido, o sea, con las caras del mismo color y en la misma disposición.

—Coge 6 cubos y forma con ellos una columna de manera que cada uno de los lados contenga los seis colores.

—Coge 8 cubos y forma con ellos un cubo de 2x2x2 que tenga en las caras derecha e izquierda un color, delante y detrás otro color y un tercer color arriba y abajo.

Casualmente (o tal vez no), por un precio muy módico puedes comprar en la red un set de 30 cubitos de madera de 3 cm de lado que, una vez coloreados convenientemente para convertirlos en cubos de MacMahon, te pueden suministrar muchas horas de instructivo entretenimiento. O sufrimiento (pero también instructivo).