El teorema de Varignon

La demostración del teorema de Viviani, del que hablábamos la semana pasada en relación con el punto de Fermat/Torricelli, es tan sencilla como elegante:

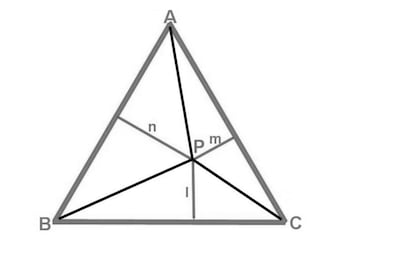
Sea el triángulo equilátero ABC de lado unidad y en su interior un punto cualquiera P. Uniendo P con los tres vértices del triángulo y llamando m, n y l a sus distancias a los tres lados, obtenemos los triángulos PAB, PAC y PBC, cuyas áreas son, respectivamente, m/2, n/2 y l/2, cuya suma es el área de ABC, que, por otra parte, llamando h a la altura del triángulo, es h/2; por lo tanto, h = m + n + l.

El paralelo de Varignon

Con respecto al teorema de Varignon, he aquí una demostración “en una línea” que vi hace unos años en la excelente página web Gaussianos:

Sea el cuadrilátero ABCD y E, F, G, H los puntos medios de sus lados, que determinan el cuadrilátero EFGH.

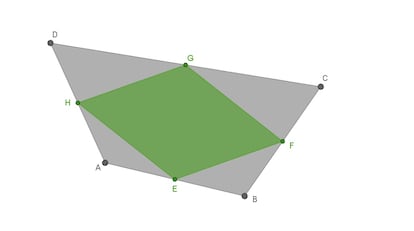
Si consideramos que todos los segmentos son vectores (imaginad las flechitas encima de cada par de letras), he aquí la demostración en una línea:

HG = HD + DG = 1/2 (AD + DC) = 1/2 AC = EF

Y del mismo modo se demuestra que HE = GF, luego el cuadrilátero EFGH es un paralelogramo, como queríamos demostrar.

Nuestro comentarista habitual Francisco Montesinos viene a decir lo mismo: “Sea ABCD un cuadrilátero. El p.m. (punto medio) del segmento AB es (A+B)/2 y el p.m. del segmento AD es (A+D)/2 y el vector diferencia de ambos es (B-D)/2, que es el mismo vector que se obtiene restando los puntos medios de CB y CD. De igual forma se demuestra que los otros dos lados que unen los p.m. correspondientes son también paralelos”.

Y, en realidad, estas ingeniosas demostraciones aún se pueden abreviar un poco más, y sin otros recursos que los de la geometría más elemental. ¿Cómo?

Otra propiedad del paralelogramo de Varignon es que su área es la mitad que la del cuadrilátero inicial (siempre que sea convexo o cóncavo, sin intersecciones). Y, además, el perímetro del paralelogramo de Varignon es igual a la suma de las diagonales del cuadrilátero inicial. ¿Puedes demostrarlo?

Geometría y papiroflexia

De la primera entrega del año ha quedado pendiente un bonito “clásico” que no me resigno a que pase inadvertido: ¿Puedes dividir un cuadrado en 5 cuadrados iguales sin más ayuda que la de una regla? Y si recurres a la papiroflexia, ni siquiera es necesaria la regla.

Y hablando de papiroflexia, ¿cómo se puede dividir una hoja de papel cuadrada en tres partes iguales, sin regla ni compás, solo mediante los dobleces adecuados?

Para este y otros problemas papirofléxicos, es interesante conocer el primer teorema de Haga, que dice:

Sea un cuadrado de vértices A, B, C, D. Si se pliega el cuadrado sobre sí mismo llevando el vértice A al punto medio del lado BC, entonces el lado AD cortará al lado CD en un punto G tal que la distancia entre C y G es igual a las dos terceras partes del lado del cuadrado.

El teorema recibe su nombre del matemático japonés Kazuo Haga, conocido sobre todo por sus minuciosos estudios geométricos sobre papiroflexia, recogidos en parte en su libro Origamics.

Y hablando de papiroflexia, ¿sabrías dibujar una pajarita de papel? No parece un problema de matemáticas ni de lógica, sino una prueba de memoria visual, y sin embargo…