Fracciones egipcias
Los antiguos egipcios expresaban los números racionales como sumas de fracciones unitarias distintas
Con respecto al problema de las 100 cápsulas, planteado la semana pasada, he aquí lo que comenta Piciencia:
“En el caso a) el que juega primero puede ganar si elige la cápsula llena, pero a cambio, si no acierta, compensa al que juega segundo al eliminar una cápsula vacía. En el b) esa compensación no se da y el primero tiene una ventaja segura. Que la compensación en a) es suficiente como para igualar las probabilidades de los dos jugadores, en la solución de MoMath se explica planteando que es un juego equivalente a asignar al principio 50/100 cápsulas a cada uno”.
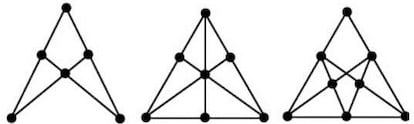
En cuanto al “problema del huerto”, no intentes mejorar la configuración de la figura de la entrega anterior: con 9 puntos, el máximo de alineaciones de 3 puntos obtenibles es 10. Con 3 o 4 puntos, obviamente, solo se puede formar una alineación de 3 puntos; con 5 puntos solo se pueden conseguir 2; con 6 puntos, 4; con 7 puntos, 6; con 8 puntos, 7; con 9 puntos, como ya hemos visto, 10… La secuencia, a medida que aumentamos el número de puntos a partir de 3, es 1, 1, 2, 4, 6, 7, 10, 12, 16, 19, 22, 26… ¿Podemos sacar alguna conclusión de esta secuencia?
La sucesión de Sylvester
No podemos despedirnos de James Joseph Sylvester y de sus problemas de alineación de puntos sin mencionar la sucesión que lleva el nombre del gran matemático británico.
La sucesión de Sylvester es una vertiginosa sucesión de números naturales (enteros y positivos) en la cual cada término es el producto de todos los anteriores más 1. Los ocho primeros términos de la sucesión, que crece de forma doblemente exponencial, son:
2, 3, 7, 43, 1807, 3263443, 10650056950807, 113423713055421844361000443…
Obsérvese que el noveno término de la sucesión difícilmente cabría en una sola línea, pues tendría… ¿cuántas cifras?
Es interesante considerar la serie de los inversos de los términos de la sucesión de Sylvester:
1/2 + 1/3 + 1/7 + 1/43…
Es fácil ver que es una serie convergente (basta compararla con otra serie convergente bien conocida: 1/2 + 1/4 + 1/8 + 1/16… y ver que sus denominadores crecen mucho más deprisa), pero ¿a qué valor converge? Sirva la siguiente figura como pista gráfica.
La serie de los inversos de la sucesión de Sylvester (o, más exactamente, cualquier subconjunto finito de sus términos) es una fracción egipcia, es decir, una suma de fracciones unitarias distintas (fracción unitaria es aquella cuyo numerador es 1 y cuyo denominador es un número natural).
Las fracciones egipcias se denominan así porque los antiguos egipcios las utilizaban recurrentemente en sus cálculos, como se desprende del papiro de Ahmes (también conocido como papiro de Rhind) y otros documentos milenarios.
Invito a mis sagaces lectoras/es a viajar al remoto pasado (unos cuatro mil años atrás) para demostrar que cualquier número racional puede expresarse como fracción egipcia. La cuestión sería trivial si se pudieran repetir denominadores (por ejemplo, 3/7 = 1/7 + 1/7 + 1/7); pero hay que tener en cuenta que en las fracciones egipcias todos los denominadores han de ser distintos.
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.
Sobre la firma
