El problema del huerto

Con respecto a los indigestos números McNugget de la semana pasada, he aquí lo que dice nuestro comentarista habitual Salva Fuster:

“Los números McNugget de 6, 9 y 20 son: 1, 2, 3, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 22, 23, 25, 28, 31, 34, 37 y 43, es decir, un total de veintidós números, siendo el 43 el mayor de ellos que no se puede conseguir.

Los números McNugget de 4, 6 y 9 son los seis siguientes: 1, 2, 3, 5, 7 y 11. En este caso el número de Frobenius-McNugget sería el 11.

Una forma sencilla de ver los números que no se pueden obtener como combinación de 4, 6 y 9 es la siguiente:

Con 4 y 6 podemos obtener cualquier número par mayor que 4.

Por otra parte, sumando 9 a cualquier par mayor o igual que 4, obtendremos cualquier impar mayor o igual que 13.

No podremos hacer los impares menores que 13, salvo el propio 9, ni tampoco podremos hacer el 2, de modo que la lista de los no conseguibles es: 1, 2, 3, 5, 7, 11″.

Otro comentarista habitual, Manuel Amorós, plantea el acertijo siguiente:

En una urna hay 100 cápsulas idénticas, una de las cuales contiene un premio.

a) Un amigo y tú vais sacando alternativamente las cápsulas, una a una, y las abrís hasta dar con la premiada. Para maximizar tus probabilidades de obtener el premio, ¿te conviene sacar en primer o en segundo lugar?

b) Misma cuestión, pero ahora las cápsulas vacías no se descartan, sino que se vuelven a meter en la urna y se mezclan con las demás.

Un sutil acertijo de aspecto inofensivo que suscitó interesantes comentarios y que me da pie a plantear una metapregunta algo capciosa: sin conocer ni buscar las respuestas a y b, ¿podemos asegurar que serán diferentes?

Y un tercer comentarista asiduo (esta semana la sección la han hecho los lectores, benditos sean), Juan José Rodríguez, relacionó sagazmente a Frobenius con el matemático británico James Joseph Sylvester, que introdujo términos tan básicos como “matriz” o “discriminante”, y que es conocido sobre todo por sus aportaciones a la geometría discreta.

El problema de la plantación de árboles

Uno de los problemas de geometría discreta abordados por Sylvester es el denominado “problema del huerto” o “problema de la plantación”, que debe su nombre a que, en la práctica, se plantea este tipo de problemas cuando se desea plantar árboles de forma que se alineen de una determinada manera. En concreto, se trata de hallar el máximo número de alineaciones rectilíneas de 3 puntos que se pueden formar situando n puntos en el plano.

Es evidente que con 3 puntos solo se puede formar una fila de 3, y con 4 puntos también, pues no hay manera de colocar el cuarto punto para formar una nueva fila de 3. ¿Y con 5, 6, 7… puntos? ¿Hay alguna relación sencilla entre el número de puntos y el máximo número de filas de 3 puntos que se pueden formar con ellos?

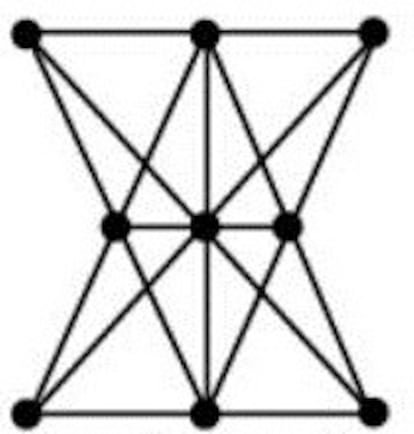
En la figura vemos una elegante configuración de 9 puntos con 10 alineaciones de 3 puntos. ¿Se puede mejorar?

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.