Números McNugget

Con respecto al problema de Frobenius, expuesto la semana pasada, he aquí la aportación de Luca Tanganelli:

“Con monedas de 3 y 5, los números n ≥ 10 de la forma 3k+1 se pueden obtener como 3(k–3)+5*2.

Los números n ≥ 5 de la forma 3k+2 se obtienen con 3(k–1)+5.

Esto deja como número de Frobenius al 7.

Generalizando, sean a y b, a≤b, las dos monedas. Si a y b tienen factor común es evidente que no existe número de Frobenius.

Si a y b son coprimos, entonces los a*i son distintos mod b para todo 0 ≤ i ≤ b–1 y similarmente para los b*j, con 0 ≤ j ≤ a–1.

Esto significa que todo número mayor o igual que a(b–1) o mayor o igual que b(a–1) podrá expresarse bajo la forma ax+by. Como a≤b, se tiene que f ≤ ab–b–1, que no está mal como cota”.

Con hipotéticas monedas de 7 y 9 euros, las cantidades enteras que no podríamos pagar con solo monedas de dichos valores sin que tuvieran que darnos cambio son: 1, 2, 3, 4, 5, 6, 8, 10, 11, 12, 13, 15, 17, 19, 20, 22, 24, 26, 29, 31, 33, 38, 40 y 47, por lo que el número de Frobenius para 7 y 9 es 47 (dejo a mis sagaces lectoras/es la comprobación de este resultado).

En cuanto a la paradoja de Bertrand, Francisco Montesinos aporta un ingenioso enfoque que da el valor 1/4 para la probabilidad de que una cuerda trazada al azar en una circunferencia sea mayor que el lado del triángulo equilátero inscrito:

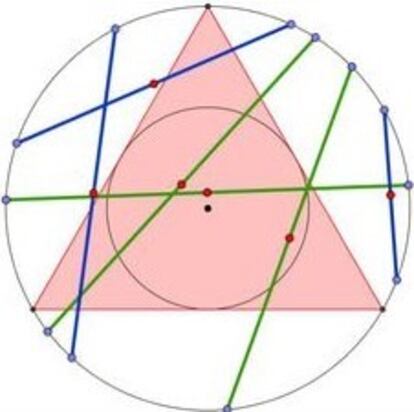
Si trazamos el círculo inscrito en el triángulo, el punto medio de una cuerda cualquiera quedará o bien dentro de ese círculo o bien fuera, y cuando quede dentro la cuerda será mayor que el lado del triángulo. Como el radio del círculo inscrito es la mitad que el del circunscrito, su área será cuatro veces menor, por lo tanto, la probabilidad de que una cuerda sea mayor que el lado del triángulo es 1/4 (en el caso de que la cuerda sea tangente al círculo inscrito, su longitud será igual a la del lado del triángulo).

Números indigestos

Mientras estaba cenando con su hijo en un McDonald’s, al matemático y experto en puzles Henri Picciotto se le ocurrió una variante de los números de Frobenius que se hizo popular como “números McNugget” (que no puedo dejar de mencionar por más que deplore que se contamine el sagrado ámbito de las matemáticas con una referencia a la comida basura). Parece ser que los McNuggets se servían en cajas de 6, 9 y 20 unidades, y cualquier cantidad de estos indigestos bocaditos que pudiera obtenerse adquiriendo cajas de estas fue denominada por Picciotto un número McNugget. Y la frobeniusiana cuestión es: ¿cuál es el máximo número de McNuggets que no se pueden obtener combinando estos tres tipos de cajas?

Actualmente las cajas de McNuggets son de 4, 6 y 9 piezas (supongo que eliminaron las de 20 por orden de las autoridades sanitarias); ¿cuál es ahora el número de Frobenius-McNugget?

Obsérvese que en este caso se parte de tres números, y no de dos, para hallar el número de Frobenius relativo a ellos, lo cual puede complicar extraordinariamente la situación; tanto, que no se conoce una fórmula general que permita hallar directamente los números de Frobenius correspondientes a tres o más números de partida.

Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.