Matemáticas para entender la asimetría del cerebro

Muchos avances en neurociencia llegaron gracias a análisis matemáticos minuciosos. Por ejemplo, Alan Hodgkin y Andrew Huxley utilizaron ecuaciones diferenciales para describir el potencial de acción, que transmite información entre neuronas, lo que les valió el Premio Nobel en 1963. Ahora es cada vez más habitual utilizar herramientas matemáticas para analizar las ingentes cantidades de datos neurales que se están obteniendo. Más allá de esto, empleando principios matemáticos fundamentales, ha sido posible respaldar conjeturas sobre el funcionamiento del cerebro planteadas desde hace décadas o siglos.

Se trata de hipótesis relevantes con amplio respaldo en la comunidad, a pesar de sumar escasas pruebas empíricas o de que aún no existan argumentos matemáticos definitivos. Recuerdan a célebres conjeturas —como el último teorema de Fermat o la hipótesis de Riemann— que retan a varias generaciones en busca de una confirmación rigurosa.

Un ejemplo es la hipótesis del cerebro predictivo: gran parte de nuestras capacidades cognitivas resultan de una presión evolutiva para anticipar nuestro entorno. El gran éxito de los llamados large language models (LLM), como el ChatGPT de OpenAI o LlaMa de Meta, respalda esta idea. Su espectacular “inteligencia” resulta de una única tarea: maximizar la probabilidad de acertar la siguiente palabra, dado un texto incompleto. Esto evidencia que la predicción permite desarrollar una cognición avanzada. Falta saber si, además, las capacidades cognitivas requieren siempre de este tipo de destreza.

Otro ejemplo que acaba de obtener respaldo matemático es la hipótesis de que una mayor complejidad cognitiva conlleva una lateralización, o ruptura de la simetría especular del cerebro. Esta idea se da por buena casi desde los comienzos de la neurociencia (llegando a libros de texto y de divulgación científica). Hace más de 150 años, el descubrimiento del área de Broca (responsable de la generación del lenguaje) constató dos hechos relevantes sobre el cerebro: que existe localización (es decir, diferentes regiones implementan distintas tareas) y que es asimétrico, ya que esta área suele localizarse en el hemisferio izquierdo. Esto llevó a postular que la lateralización resulta de la avanzada inteligencia humana. Con el tiempo se descubrieron ejemplos de asimetría en muchas otras especies, suavizando la hipótesis: una mayor complejidad cognitiva ejerce una presión evolutiva hacia la lateralización cerebral.

Hasta hace poco esto solo estaba apoyado por observaciones anecdóticas. Es difícil obtener más evidencia empírica debido al reto de medir la asimetría cerebral y cuantificar la complejidad cognitiva. Además, no existía un marco teórico adecuado que permitiera plantear —no ya responder— la conjetura de manera rigurosa.

Un nuevo trabajo publicado en Physical Review X ofrece este marco y aporta un argumento matemático robusto que respalda la hipótesis. Para ello se emplea un modelo matemático, inspirado por la ciencia de sistemas complejos, en el que módulos y circuitos neuronales son reducidos a unidades abstractas. Estas unidades encapsulan la complejidad de la cognición emergente, la probabilidad de que los circuitos neuronales cometan errores y los costes de utilizar estos circuitos, como el gasto metabólico de coordinar ambos hemisferios, o la energía disipada por toda operación irreversible.

La clave del argumento matemático reside en un conflicto entre los llamados operadores lógicos, expresiones matemáticas cuyo resultado es un valor booleano (verdadero o falso). Partimos de una tarea cognitiva sencilla, que puede ser resuelta con un circuito neuronal irreducible —es decir, que no puede descomponerse en subtareas—. El cerebro podría emplear una única copia de este circuito, ubicada en uno u otro hemisferio (a lo que se asigna el operador lógico XOR); utilizar dos copias coordinadas del mismo circuito, ubicadas cada una en un hemisferio (a lo que se asocia la expresión AND); o alguna combinación intermedia (OR). La primera opción es más económica, pero la segunda puede ser más robusta frente a fallos de las neuronas.

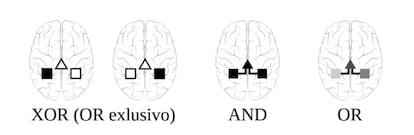
Con todas las configuraciones posibles se realiza un cálculo utilitario que tiene en cuenta costes y beneficios. Esto permite elaborar un mapa que detalla cuándo se prefieren soluciones lateralizadas frente a las simétricas en función de los parámetros del modelo, que son los costes y una tasa de error. Un primer resultado es que no existen configuraciones intermedias: siempre se dará bilateralidad o una ruptura total de la simetría.

Un segundo resultado, y con él la solución a la hipótesis central, aparece al considerar tareas cognitivas complejas. En el modelo, estas constan de diversas subtareas y requieren circuitos compuestos para ser implementadas. Esto se traduce en una operación AND recursiva: para beneficiarse de la cognición avanzada es necesario implementar sin error una subtarea, y otra, y otra, etc. Al introducir este nuevo operador en el cálculo utilitario se altera el mapa: regiones que antes demandaban bilateralidad pasan a preferir lateralización, mostrando con contundencia la existencia de presiones evolutivas para perder la simetría cerebral a medida que aumenta la complejidad cognitiva.

También aparece una región que prefiere lateralización para tareas simples, pero exige circuitos duplicados para tareas complejas. Así, la complejidad cognitiva puede promover la evolución de nuevas redundancias, funcionando como un motor evolutivo que genera o rompe simetrías en circunstancias complementarias. El marco matemático indica cuándo se dará cada posibilidad, según el gasto metabólico del sustrato neuronal, su tasa de error y la complejidad de la tarea contemplada.

Estos condicionantes matemáticos, y la estructura inescapable de ciertos objetos abstractos, constriñen la realidad física y la materialización biológica de nuestras capacidades cognitivas.

Tomándonos las matemáticas en serio, es posible restringir qué diseños son posibles y probables en un sustrato neuronal y las representaciones mentales correspondientes. Y, mientras llegan más pruebas empíricas, esta hipótesis central de la neurociencia descansa ahora en un marco analítico robusto.

Luis F Seoane es investigador del Consejo Superior de Investigaciones Científicas en el Centro Nacional de Biotecnología y parte del Grupo Interdisciplinar de Sistemas Complejos de Madrid

Ágata Timón G Longoria es coordinadora de la Unidad de Cultura Matemática del Instituto de Ciencias Matemáticas (ICMAT)

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.