Sangaku

Es fácil demostrar, como se pedía la semana pasada, que 42 es la constante mágica (CM) de un cubo mágico de 3x3x3 en cuyas celdillas se colocan los números del 1 al 27 de forma que todas las filas y columnas, así como las diagonales que pasan por el centro, sumen lo mismo, pues 1 + 2 + 3… + 25 + 26 + 27 = 378, y puesto que podemos dividir el cubo en 9 columnas y todas han de sumar lo mismo, CM = 378/9 = 42.

Los números para situar en las 27 casillas no tienen por qué ser del 1 al 27, por lo que invito a mis sagaces lectoras y lectores a ponerse las gafas 3D e investigar otras posibilidades y características del cubo mágico de orden 3.

O de orden 4, 5…

¿De cuántas maneras distintas podemos dividir un cuadrilátero en triángulos mediante diagonales que no se corten? De dos, obviamente: uniendo uno u otro par de vértices opuestos. ¿Y un pentágono? De cinco, pues desde cada vértice podemos trazar dos diagonales uniéndolo con los vértices no contiguos, dividiendo de este modo el pentágono en tres triángulos. ¿Y un hexágono? La respuesta está implícita en los comentarios sobre el “aburrido” número 42 del artículo de la semana pasada, pero os invito a buscarla sin recurrir a esa cercana ayuda.

Si las diagonales pueden cruzarse, aumenta considerablemente el número de triángulos en que se puede dividir un polígono. Así, trazando las dos diagonales de un cuadrilátero lo dividimos en cuatro triángulos. ¿Cuál es el máximo número de triángulos en que podemos dividir un pentágono trazando sus diagonales? ¿Y un hexágono? ¿Varía dicho número máximo si los polígonos son o no regulares, y si son o no convexos?

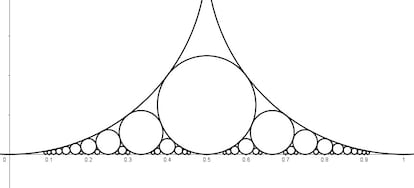
Círculos de Ford

Trazamos dos circunferencia de radio unidad tangentes entre sí y tangentes ambas a una recta, y luego una tercera circunferencia tangente a las dos anteriores y a la recta. ¿Cuánto mide el radio de esta tercera circunferencia?

Si seguimos trazando circunferencias —cada vez menores— tangentes a la recta y a las sucesivas circunferencias, como en un tamiz de Apolonio en el que una de sus tres circunferencias generatrices tiene radio infinito (la recta), obtenemos una familia de círculos de Ford.

La definición matemática de círculo de Ford puede resultar un tanto disuasoria para quienes tienen fobia a las fórmulas, pero la idea es más sencilla de lo que parece a primera vista. Un círculo de Ford es aquel que, en unos ejes de coordenadas, tiene el centro en el punto (p/q, 1/2q 2 ) y cuyo radio es 1/2q 2 , donde p y q son números enteros primos entre sí (o, dicho de otro modo, donde p/q es una fracción irreducible). Como el radio del círculo es igual a la ordenada del centro, los círculos de Ford, en su representación habitual, son tangente al eje de las abscisas, es decir, a una recta horizontal.

Los círculos de Ford, denominados así en honor del matemático estadounidense Lester R. Ford, que los estudió en la primera mitad del siglo XX, presentan interesantes propiedades que veremos en otra ocasión; de momento, bástenos saber que algunos precedentes aparecen en los sangaku japoneses, rompecabezas geométricos grabados en tablillas de madera que se depositaban en los templos como ofrendas a los dioses y retos a los visitantes.

En un sangaku del siglo XIX se ven tres círculos de distintos tamaños tangentes entre sí y tangentes los tres a una recta, y se pide el radio del menor conociendo los radios de los otros dos. ¿Pueden mis sagaces lectoras y lectores hallar una terna de círculos que cumplan esta condición y cuyos radios sea números enteros?

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.