Así se descubrieron mosaicos de variedad infinita con una sola pieza

Los teselados forman uno de los más fecundos puntos de encuentro entre las matemáticas y el arte. Estos recubrimientos del plano por copias de una o varias formas (las piezas, o teselas) constituyen técnicas decorativas usadas por numerosas culturas desde la antigüedad. Entre los ejemplos más bellos se hallan los mosaicos que adornan varios patios y salones de la Alhambra, y que inspiraron a quien fue uno de los más creativos exploradores del potencial estético y matemático de los teselados: Maurits C. Escher.

Tras siglos de estudio de estas construcciones geométricas, decir algo novedoso acerca de los teselados podría parecer improbable. Sin embargo, esto es precisamente lo que consiguieron cuatro investigadores en 2023: descubrieron un nuevo tipo de teselas, cuya existencia había sido objeto de especulaciones desde hacía más de medio siglo. Se trata de las llamadas monoteselas aperiódicas, o, como las apodó el matemático Ludwig Danzer, las einstein (del alemán ein stein, que significa “una piedra”).

Una colección de piezas planas permite formar un teselado si es posible cubrir todo el plano pegando copias de estas piezas de forma que no se solapen ni quede ningún hueco entre ellas. Antes de pegar cada pieza, se puede desplazar con movimientos de tres tipos en el plano: traslaciones, rotaciones y reflexiones (es decir, dar la vuelta a la pieza para pegarla por su otra cara).

Entre los ejemplos más sencillos se encuentran los teselados regulares, formados a partir de una única pieza que es un polígono regular. Se sabe, al menos desde los trabajos de Johannes Kepler recogidos en su famosa obra Harmonices Mundi (de 1619), que solo tres polígonos regulares permiten construir este tipo de teselado: el triángulo equilátero, el cuadrado y el hexágono regular.

Si en la colección inicial hay varias piezas distintas, de tipos más generales (como polígonos no regulares, o incluso formas curvadas), entonces se puede obtener una infinitud de diversos teselados, que dan lugar a múltiples exploraciones artísticas, como en los ejemplos de la Alhambra. No obstante, muchos de estos teselados tienen una complejidad limitada, en el sentido de que se repiten, son periódicos. Un teselado es periódico si incluye una región que permite, trasladándola, obtener la totalidad del teselado (sin rotaciones ni reflexiones). Un teselado que no tiene esta propiedad se llama teselado no-periódico.

Con algunas formas, como el hexágono regular, solo se pueden hacer teselados periódicos. Por otro lado, hay formas que pueden generar teselados periódicos y también no-periódicos. Por ejemplo, con un rectángulo de proporciones 2:1, podemos hacer un teselado periódico y otro no-periódico. Surge entonces la pregunta de si existen colecciones finitas de piezas que solo permiten hacer teselados no-periódicos. Tales piezas se llamarían teselas aperiódicas.

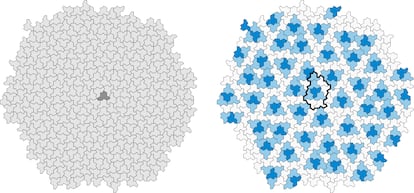
Resulta que sí existen. Se empezaron a conocer ejemplos concretos solo a partir de los años sesenta, cuando Robert Berger ―en su tesis doctoral en 1964― dio una colección de 20.426 piezas que, conjuntamente, solo permiten crear teselados no-periódicos. Este avance inició una intensa búsqueda, por varios matemáticos, de colecciones de teselas aperiódicas con el mínimo número posible de piezas. En 1974, el físico y matemático Roger Penrose consiguió ―inspirándose en parte en los trabajos de Kepler― hallar una colección de teselas aperiódicas con solo dos piezas, estableciendo así lo que fue el récord durante casi medio siglo. Perduró desde entonces el enigma de si existe alguna monotesela aperiódica, es decir, una sola pieza que permite teselar el plano únicamente de modo no-periódico.

En 2023, David Smith, Joseph S. Myers, Craig S. Kaplan, y Chaim Goodman-Strauss, dieron con una pieza de este tipo. La primera monotesela aperiódica que descubrieron tiene una forma tan simple que dejó atónitos a muchos expertos en este tema. Consiste en un polígono de 13 lados, que pronto fue bautizado por sus descubridores como el sombrero. Ahondando en su estudio, los autores descubrieron también que, lejos de ser única, esta forma es solo una de entre una infinitud de posibles formas que también constituyen monoteselas aperiódicas.

Este descubrimiento no puso fin a esta línea de investigación, sino que pronto surgieron nuevas cuestiones. Por ejemplo, en el teselado del sombrero se usan todas las tres operaciones permitidas para cubrir el plano: traslación, rotación y reflexión. Esto dio lugar a la pregunta de si existen monoteselas aperiódicas cuyos teselados solo usan traslación y rotación. Los mismos cuatro investigadores descubrieron otra nueva forma geométrica que dio respuesta positiva a esta pregunta.

Más allá de las matemáticas, las teselas aperiódicas tienen interés en física y química, especialmente por su relación con las estructuras llamadas cuasicristales. Los cuasicristales fueron descubiertos por el científico Dan Shechtman en los años ochenta, en trabajos que le valieron el Premio Nobel de Química en 2011. Pocos años después de su descubrimiento, se empezaron a estudiar conexiones entre ciertos tipos de cuasicristales y los teselados de Penrose.

Pablo Candela es científico titular del CSIC en el Instituto de Ciencias Matemáticas (ICMAT).

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.

Edición, traducción y coordinación: Ágata Timón García-Longoria. Es coordinadora de la Unidad de Cultura Matemática del Instituto de Ciencias Matemáticas (ICMAT)