Desafío criptográfico: un misterio oculto en cuadraditos blancos y negros

Después de que Jordi entendiera en el desafío anterior en qué consistía el cifrado Vernam o One Time Pad, continuó con la videollamada con Paz, su madre.

―Mamá, lo de la criptografía visual, ¿qué tiene que ver? Mi tutor, Paolo, insiste en que es más o menos lo mismo que el Cifrado Vernam, pero no veo por dónde va…

Paz sonreía ante la impaciencia de su hijo.

—Pues parte de la idea anterior, solo que aquí la información no está codificada en forma de cadena binaria, sino como una imagen. Por tanto, no se tienen que hacer operaciones matemáticas para recuperar el secreto: se ocupa el ojo humano. Te mando unas fotos al móvil.

—Intenta superponerlas. Sólo tienes que imprimir en un papel un poco fino y las pones una encima de la otra en el vidrio de una ventana. Y obtendrás lo siguiente:

Ahora, fíjate: si tomas la primera transparencia y la superpones con la que te mande a continuación, verás que obtienes una letra distinta. ¿Cuál es?

Jordi pensó que mejor lo dejaba para más tarde… su madre seguía hablando, y no quería perder el hilo.

—Pero hay algo más —añadió Paz—, la criptografía visual a menudo incluye un ingrediente esencial para todo buen criptógrafo: la desconfianza.

—¿¿La desconfianza??

—Eso es. Si el emisor de un mensaje ni siquiera se fía del todo de un receptor concreto, puede repartir entre varios destinatarios la capacidad de descifrar. Para ello, la imagen que hace de clave va “fragmentada” en varias transparencias: para recuperarla será necesario poner cuidadosamente las transparencias-clave una encima de la otra. Luego, situando esta “pila” sobre la transparencia-mensaje, puede verse la imagen descifrada.

Jordi estaba intrigado.

―Pero, ¿cómo se fabrican estas imágenes a partir de la inicial?

―No es difícil. Para repartir un píxel negro de la imagen original deberemos elegir para cada una de las transparencias una de las dos combinaciones de píxeles siguiente:

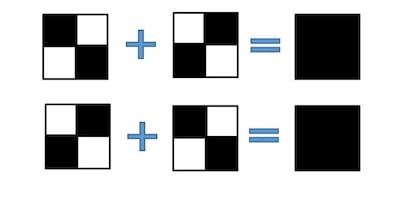
La elección de una combinación o de otra se tiene que hacer aleatoriamente. De la misma manera se hace para repartir un píxel blanco, usando eso sí un material tal que al superponer dos transparencias negras se obtenga el color blanco (como eso no es fácil de reproducir en papel, que será el material que utilicen los lectores, jugaremos con los tonos de gris). Así, para cada píxel original blanco debemos elegir aleatoriamente entre una de estas dos descomposiciones:

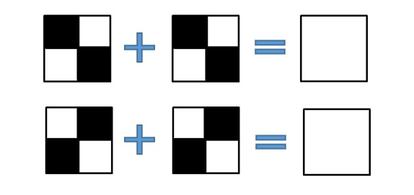
―Pero es un trabajo pesadísimo…

―Claro: se tiene que implementar en programas que lo hagan rápidamente. La imagen original anterior tiene 100 píxeles. Pero, ¿acaso alguien cifra a mano un mensaje para que viaje de forma segura por Internet? Ahora que ya lo entiendes, te planteo un nuevo desafío: ¿puedes jugar con estas transparencias a ver qué imagen hay escondida y qué combinaciones pueden recuperar la imagen secreta?

Paz colgó, pensando en que podía incluso haberle planteado un reto más exigente a Jordi; con el que quizá se atreva alguno de nuestros lectores. ¿Os animáis a enviarnos un mensaje cifrado con este método (y la clave asociada, para que podamos descifrar)? Más aún, ¿se os ocurre otro formato, no visual, por el que podamos implementar el Cifrado Vernam utilizando otro de nuestros sentidos? Nos encantará ver vuestras propuestas, y comentaremos las mejores con la solución de este reto.

Germán Sáez Moreno es investigador del grupo MAC y profesor de Matemática Aplicada en la Universitat Politècnica de Catalunya.

SOLUCIÓN AL DESAFÍO ANTERIOR

PRIMER EJERCICIO

La primera pregunta al lector del anterior desafío era si podríamos obtener cualquier mensaje original probando claves distintas. Y la respuesta es que sí, dado un cifrado, podemos hacer que “encaje” con cualquier mensaje m enviado, fijando como clave la cadena c ⨁ m, pues obviamente si a c le sumamos la cadena de bits c ⨁ m obtendremos, de nuevo, el mensaje de partida, m. Esto ocurre por ser la operación XOR autoinversa (y los dos “c” cancelarse).

Para el ejemplo concreto propuesto, basta ver que

c⨁k’= 01101 11010 00001 10101+01111 11010 00100 10001=00010 00000 00101 00100

es decir, obtenemos la palabra CAFÉ.

SEGUNDO EJERCICIO:

El segundo desafío consistía en descifrar un mensaje oculto sabiendo que la clave era “un testigo impagable de los tiempos”, y el mensaje original estaba relacionado con un dios del mar. Como pista adicional, ambos términos estaban relacionados con el lugar en el que se encontraba el protagonista del desafío (Salerno, Italia).

Muchos lectores han encontrado la solución y nos la han enviado a nuestro correo. A algunos, como a Efraim, Zoe y Gonzalo o Mariona, les ha ayudado conocer la zona; otros, como Luis, Ramiro o Manolo han probado posibles claves como Vesubio, Neptuno e incluso pizzero. La correcta, y la que se ajusta al “testigo de los tiempos”, era POMPEYA que se codifica como:

K = 10000 01111 01100 10000 000100 11001 00000

Sumada a la cadena cifrada

C = 00000 01111 01000 00011 10000 01100 01100

Obtenemos el mensaje enviado:

10000 00000 00100 10011 10100 10101 01100

que se decodifica como PAESTUM (antigua ciudad de Poseidonia, en la provincia de Salerno).

En el enunciado había otra “pista encubierta”, pues al ser la primera letra del cifrado 00000, necesariamente clave y mensaje enviado debían ser palabras que empezasen por la misma letra. Pensamos que esta pista podía ser útil para reducir el chequeo de posibles claves; si uno utiliza “Google/Wikipedia” y busca dos palabras de 7 letras relacionadas con Salerno y que empiecen por la misma letra, las opciones se reducen mucho ….

Este desafío se centra en el llamado Cifrado Vernam, propuesto a principios del Siglo XX por Gilbert S. Vernam, ingeniero de la compañía telefónica AT&T. Este método sirvió de base para la definición por parte de Claude Shannon de la noción de cifrado perfecto. Rebautizado como One-time Pad, Shannon lo introdujo en su famoso trabajo “Communication Theory of Secrecy Systems” Bell System Technical Journal 28(4) pp. 656–715, donde demostraba además que este método es seguro siempre que las claves sean de un solo uso y de la misma longitud que los textos a cifrar.

Puedes seguir a EL PAÍS TECNOLOGÍA en Facebook y Twitter o apuntarte aquí para recibir nuestra newsletter semanal.