El acertijo de la cámara secreta

Jorge y Clara trabajaban desde hacía meses como arqueólogos en una pirámide precolombina al sur del Yucatán. Llevaban semanas intentando entrar en una cámara secreta. Pero para hacerlo debían resolver un acertijo que podría conducirles al éxito o a la muerte.

Ocho tribus se habían disputado el poder en región. Un sacerdote pacificador, jefe de una de las tribus, consiguió establecer una alianza que firmaron siete de ellas, que pasaron a custodiar la pirámide. La octava tribu se consideró maldita. Cada tribu aparecía en distintos restos arqueológicos representada a través de una figura cuadrada, que contenía una terna de símbolos. Por ejemplo, esta era la tablilla de una de las tribus:

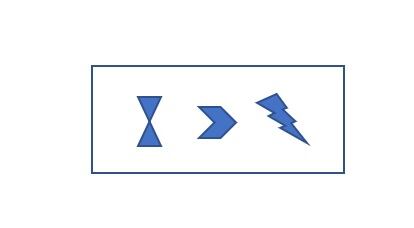
La puerta de la cámara en la que querían entrar tenía en el suelo una especie de tablero dibujado, con filas y columnas indexadas exactamente por esos símbolos, en la que podía encajarse, para cada posición de fila y columna, una única piedra con la forma de uno de los cinco símbolos distintos que se habían encontrado. Por anteriores excavaciones, se sabía que había que interpretar los tres símbolos de cada tablilla como fila-columna-símbolo. La tablilla citada más arriba, por ejemplo, encajaría así en el tablero.

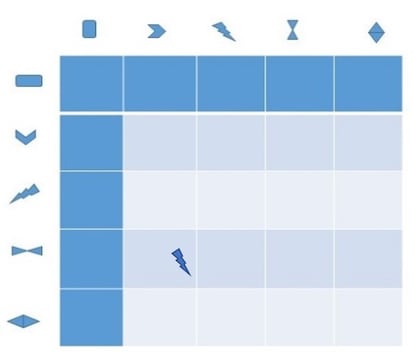
Jorge y Clara sabían que si completaban correctamente el tablero, esto es, dejando solo vacía la casilla correspondiente a la tribu maldita, se activaría un resorte que abriría la puerta a la cámara secreta. Si, por el contrario, introducían la piedra asociada a la tribu maldita, serían atravesados por los dardos preparados para ahuyentar a los saqueadores de pirámides.

Así pues, su plan era rellenar la tabla usando primero las figuras que indicaban las tablillas correspondientes a las tribus aliadas, para luego seguir añadiendo símbolos de alguna forma, hasta solo dejar una casilla sin figura. Dos eran, pues, las cuestiones a resolver:

- Había una tribu maldita entre las ocho, y era crucial excluir su tablilla…pero, ¿cómo identificarla?

- Suponiendo descartada la tablilla maldita y una vez incluidas las siete casillas elegidas ¿serían capaces de rellenar el resto de las casillas del tablero?

Insertando los símbolos de las ocho tablillas correspondientes a las ocho tribus, dibujaron el tablero parcialmente relleno en una pizarra.

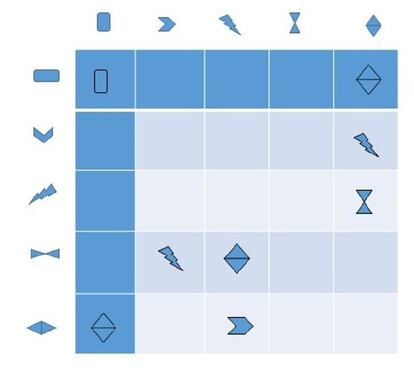
La primera casilla del tablero se correspondía con la tablilla de la tribu del sacerdote pacificador; así que, al menos, esa estaría bien colocada.

- Esa tablilla se queda – dijo Jorge taxativo. – Ahora a ver qué pasa con las demás. Y, para hacerlo más fácil, usemos los números del uno al cinco, en vez de los símbolos:

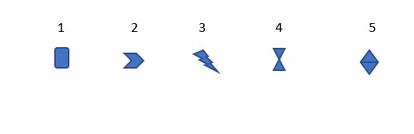
De ese modo, añadiendo las ocho tablillas y usando la codificación numérica, les quedó en la pizarra una especie de sudoku:

Jorge parecía cada vez más preocupado.

- ¿Qué tablilla descartamos, Clara? Una equivocación resultaría fatal….

Clara se puso a buscar en internet información sobre “sudokus precolombinos”, con escaso éxito. Pero encontró una página muy interesante que hablaba de algo llamado cuadrados latinos.

- Fíjate en esto, Jorge – le dijo- un cuadrado latino es una tabla con igual número de filas que de columnas, que se rellena con los números enteros {1,2,…,N} cumpliendo que en cada fila y en cada columna aparece cada uno de los números {1,2,…,N} exactamente una vez.

- Y aún hay más. Los cuadrados latinos sirven para compartir secretos. Hay algo llamado “conjuntos críticos”, que son justamente conjuntos de posiciones que sólo pueden completarse de una manera para formar un cuadrado latino, igual que el sudoku de un periódico solo tiene una solución. Así, se puede repartir un conjunto crítico entre varias personas obligándoles a colaborar para reconstruir el cuadrado porque, además, los conjuntos críticos son minimales: si se tiene sólo una parte del conjunto crítico, resulta que hay más de una manera de completar el tablero, con lo que no se sabe cuál es la solución correcta.

- Clara, no estoy seguro de estar entendiendo todo – se impacientó Jorge – tú ayúdame a decidir cómo eliminar una tablilla y más vale que no nos equivoquemos. Escribamos de nuevo la codificación numérica de las tablillas -

Clara no se hizo de rogar.

- Esto es lo que tenemos:

T1=(4,3,5) T2=(3,5,4) T3=(4,2,3) T4=(1,5,5) T5 = (5,3,2) T6=(1,1,1)T7=(2,5,3) T8=(5,1,5)

- El desafío consiste en eliminar una de las ocho figuras de la posición inicial, que se corresponderá con la tribu maldita. Y rellenar el resto de la tabla… - a Clara ahora le brillaban los ojos- sé que nos jugamos la vida, pero creo que funcionará el método que se me acaba de ocurrir…

Los desafíos criptográficos se publicarán cada 15 días. Los lectores pueden dejar sus soluciones y debatir sobre el problema en los comentarios de esta página, por lo que se recomienda a quien quiera resolverlo por sí mismo no leerlos hasta haber descifrado el enigma. También pueden enviar sus respuestas al correo desafioscriptograficos@gmail.com. En cada nuevo desafío publicaremos la solución del anterior, acompañada de un comentario con algunas ideas originales o inspiradoras que hayamos recibido.

María Isabel González Vasco es catedrática de Matemática Aplicada de la Universidad Rey Juan Carlos e integrante de la Junta de Gobierno de la Real Sociedad Matemática Española.

SOLUCIÓN AL DESAFÍO ANTERIOR

Las funciones hash son aplicaciones que asignan a cada valor de un cierto conjunto de salida un valor resumen que (típicamente) pertenece a un conjunto mucho más pequeño. Formalmente, de hecho, se definen como aplicaciones que toman una cadena binaria (de ceros y unos) de cualquier longitud y la resumen en una cadena de longitud fijada. Dicha longitud final se incluye en las implementaciones como parte del nombre de la propia función hash (ver, por ejemplo, el caso de las funciones de la familia SHA o BLAKE ). A menudo se utilizan para realizar comprobaciones rápidas (verificar si dos valores coinciden, mirando si sus resúmenes lo hacen) pero su papel fundamental es proporcionar pruebas de integridad, es decir, ayudan a detectar modificaciones en mensajes o código. Por ejemplo, en esta imagen vemos la página desde la que puede descargarse un programa para estudiar criptografía, donde se incluyen los resúmenes para cada descarga usando la función hash SHA256.

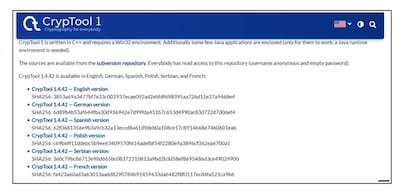
De este modo, un usuario que se baja, por ejemplo, el programa Cryptool 1.4.42 en Español, debería comprobar (ejecutando SHA256 en su ordenador) que el resumen del código obtenido coincide con la cadena de bits que aparece en la página (escrita en hexadecimal):

62f0681356e9b3a9cb32a13eccd8a61d9deb0a108ce17c8914668e7460601eab

Para que una función hash sea criptográficamente útil, se exigen dos condiciones:

- Eficiencia: los resúmenes han de ser fáciles y rápidos de calcular con mínimos recursos computacionales (un móvil, un ordenador de sobremesa, etc.)

- Resistencia a colisiones: no debe ser posible calcular eficientemente dos valores iniciales con el mismo resumen. Esto, en particular, también implicará que es difícil calcular un valor con el mismo resumen que otro dado, o revertir la aplicación de la función (dado un resumen, calcular un valor inicial asociado)

En el anterior reto, la función hash propuesta realiza una sencilla operación; quedarse con el resto al dividir cada número entre 1024. Hay 1024 restos posibles {0,…, 1023}. Es una función realmente mala, con lo que respecta a la resistencia a colisiones. Como sólo hay 1024 resúmenes, a lo sumo, se encontraría una repetición cuando entró el espectador 1025 (y, como mínimo, tuvieron que entrar dos espectadores en el recinto para que se produjese una colisión entre sus resúmenes).

Respondamos ahora a las demás preguntas; si queremos saber cuántas entradas, dentro del aforo permitido, tenían como resumen el mismo que el número 4410, tenemos que contar los números de la forma 4410 + K(1024), con K un entero, que estén entre 1 y 10900. Sirve tomar K = {-4,…, 6}, luego hay 11 entradas, que en concreto son:

En cuanto al número de entradas con idéntico identificador pero menores que 99999, serían, razonando igual, todos los números de la forma 4410 + K(1024) , con K un entero, que estén entre 1 y 99999. Podemos por tanto tomar K= {-4,…,93}, luego hay 98.

Puedes seguir a EL PAÍS TECNOLOGÍA en Facebook y Twitter o apuntarte aquí para recibir nuestra newsletter semanal.