Del cuadrado mágico al sudoku

Puesto que se puede formar un cuadrado mágico de orden n con los n² primeros números naturales, también se podrá formar con cualesquiera n² números consecutivos, puesto que si le sumamos un mismo número x a todos los de un cuadrado mágico, el cuadrado seguirá siendo mágico (con la constante aumentada en nx).

Con los nueve primeros números impares se puede formar un cuadrado mágico de constante mágica 27: 15, 1, 11; 5, 9, 13; 7, 17, 3 (las comas separan los números de una misma fila, y los puntos y coma separan una fila de otra).

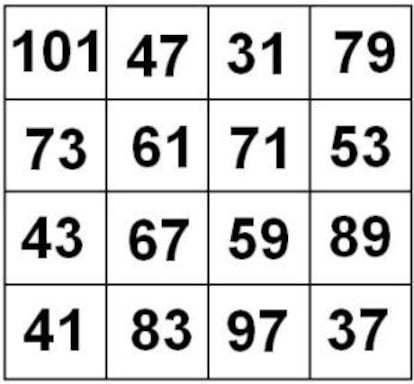
Se pueden formar cuadrados mágicos con números primos, aunque no es fácil hallarlos. Un ejemplo se puede ver en la imagen de la derecha:

En este caso, el más difícil todavía sería formar un cuadrado mágico con números primos consecutivos; de momento, me limitaré a decir que es posible.

Los cuadrados mágicos están estrechamente emparentados con los cuadrados latinos, en los que n números (u otros signos) se repiten en una cuadrícula de nxn de forma que cada número aparezca una y solo una vez en cada fila y cada columna. Se llaman cuadrados latinos porque Leonhard Euler los estudió utilizando caracteres latinos en lugar de números (aunque no fue él quien los inventó: los primeros ejemplos conocidos se remontan a un manuscrito árabe del siglo XIII).

Obsérvese que el popular sudoku (una vez resuelto correctamente) es un cuadrado latino de 9x9, con la condición adicional de que en cada subcuadrícula de 3x3 también tienen que estar los dígitos del 1 al 9 una y solo una vez.

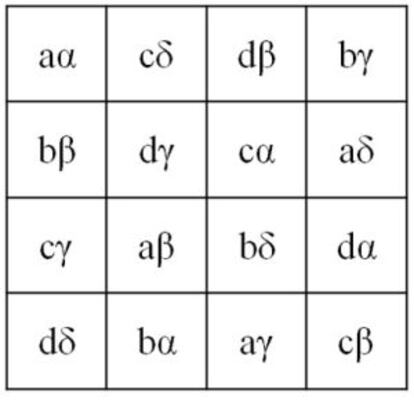
Una variante especialmente interesante, y con numerosas aplicaciones, es la de los cuadrados grecolatinos. Un cuadrado grecolatino de orden n es una cuadrícula de nxn en la cual hay en cada casilla un par ordenado de los números 1, 2, 3… n (u otros signos), de forma que los dos cuadrados formados solo por los primeros términos de cada par y solo por los segundos sean cuadrados latinos, y cada una de las n² posibles parejas de números aparezcan una y solo una vez en la cuadrícula. Se llaman así porque Euler los estudió utilizando, en vez de números, caracteres latinos para los primeros términos y griegos para los segundos, como en el ejemplo de la izquierda.

Y ahora, aunque no parezca venir muy a cuento, un toque de poesía. La sextina es una curiosa composición poética en la que se parte de una estrofa de seis versos endecasílabos que no riman entre sí, y las seis palabras finales de los versos se repiten en otras cinco estrofas de seis versos, pero siempre ocupando lugares distintos: en la segunda estrofa, la terminación del último verso de la primera estrofa pasa al primer lugar, con lo que la primera terminación se convierte en la segunda; la penúltima pasa al tercer lugar, con lo que la segunda se convierte en la cuarta; la antepenúltima pasa al quinto lugar y la tercera se convierte en la sexta. Veamos, a modo de ejemplo, las dos primeras estrofas de Apología y petición, una famosa sextina de Jaime Gil de Biedma:

¿Y qué decir de nuestra madre España,

este país de todos los demonios

en donde el mal gobierno, la pobreza

no son, sin más, pobreza y mal gobierno

sino un estado místico del hombre,

la absolución final de nuestra historia?

De todas las historias de la Historia

sin duda la más triste es la de España,

porque termina mal. Como si el hombre,

harto ya de luchar con sus demonios,

decidiese encargarles el gobierno

y la administración de su pobreza.

Para determinar el orden de las terminaciones en la tercera estrofa, hacemos con la segunda lo mismo que hemos hecho con la primera, y así sucesivamente…

¿Tiene algún sentido hablar de las sextinas en este contexto?

¿Se pueden colocar los reyes, caballos, sotas y ases de una baraja formando un cuadrado de 4x4 tal que cada fila y cada columna contenga todas las figuras y todos los palos? Y si lo conseguimos, ¿qué habremos construido?

Además de constituir un llamativo diseño para un edredón, ¿qué representa la colorista ilustración de portada?

Carlo Frabetti

Escritor y matemático, miembro de la Academia de Ciencias de Nueva York, ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’