El joven se lleva el torneo
El ganador del tercer desafío matemático del verano de EL PAÍS es Carlos de Lorenzo, de Madrid

Manuel Abellanas, de la Universidad Politécnica de Madrid, resuelve el tercer desafío matemático que este verano planteamos a nuestros lectores (puede ver aquí el vídeo). Una vez realizado el sorteo entre las respuestas correctas, de las 335 recibidas, el ganador de la colección de libros Grandes Ideas de la Ciencia ha sido Carlos de Lorenzo, de Madrid.
Para evitar confusiones y en atención también a nuestros lectores sordos incluimos la solución por escrito a continuación:
La respuesta al reto que planteábamos es que ganará el jugador más joven. La razón es que, en las condiciones del desafío, siempre se pueden dibujar 26 líneas y no más. Por tanto, al participar cinco jugadores, tras cinco rondas, habrán dibujado 25 líneas y la última la dibujará el jugador más joven por ser quien comienza cada ronda.
Veamos por qué es posible dibujar 26 líneas:
Denotemos L(P) al número de líneas que se pueden dibujar con P puntos. Nuestro objetivo es ver que L(11)=26. Para ello empecemos analizando qué pasaría si el número de puntos es menor.
Si hay solo 4 puntos, la triangulación será como esta

y, por tanto, L(4) = 5
Si hay 5 puntos, obtendremos una triangulación como una de éstas
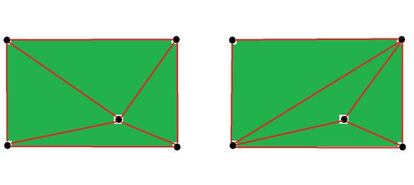
Y, por tanto, L(5) = 8.
Con 6 puntos se pueden obtener más triangulaciones diferentes, pero observa que en todas ellas hay once líneas, por lo que L(6) = 11.
El número de líneas que se obtienen para 4, 5, 6,… puntos es la sucesión 5, 8, 11, … Ya se ve que cada vez que se añade otro punto, el número de líneas aumenta tres unidades. Y, como el valor para cuatro puntos es cinco, resulta que el valor para P líneas es L(P) = 5+3(P-4), que es lo mismo que L(P)=3P-7. Esta fórmula da el valor 26 para P = 11.
Solo nos falta demostrar que la fórmula L(P) = 3P-7 se cumple para cualquier valor de P mayor que 4:
Como hemos visto, para 4, se cumple. Vamos a ver que si se cumple la fórmula para un valor k mayor o igual que 4, entonces se cumple para el siguiente valor k+1. Así se cumplirá para cualquier valor (incluido el 11 que es el que nos interesa).
Supongamos pues que la fórmula se cumple para k puntos y supongamos que ahora tenemos k+1 puntos, k mayor o igual que 4.
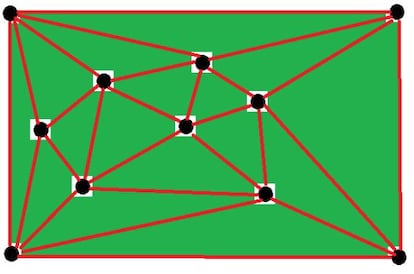
Si borramos uno de los puntos interiores y las líneas que salen de él, nos quedará un hueco en el dibujo con forma de polígono.
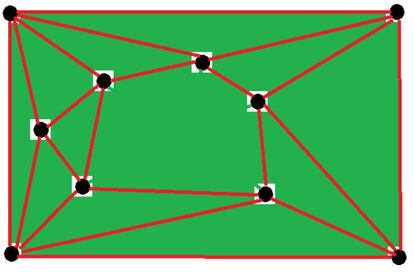
Si salían del punto borrado m líneas, el hueco será un polígono de m vértices.
No es difícil comprobar que un polígono con m vértices se descompone en triángulos (se triangula) dibujando m-3 de sus diagonales (en el ejemplo del dibujo el hueco tiene 5 vértices y necesita 2 diagonales para ser triangulado).
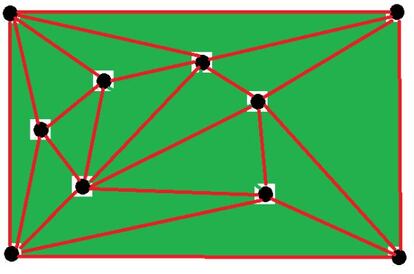
Triangulando el hueco que queda tras borrar el punto y las líneas que salen de él, completamos una triangulación de k puntos. Como estamos suponiendo que para k puntos la fórmula se cumple, el número de líneas que tendrá esta triangulación es L(k)=3k-7. Pero, como hemos visto, el número de líneas de la triangulación de los k puntos es tres unidades menor que el de la triangulación de los k+1 puntos (pues habíamos borrado m líneas y hemos tenido que añadir solo m-3 para completar la triangulación). Por tanto, el número de líneas de la triangulación original de los k+1 puntos debe ser 3k-7+3, es decir, 3(k+1)-7, que corresponde al valor de la fórmula para P=k+1.
Bonito, ¿verdad? De esta forma, no sólo hemos obtenido el resultado para 11 puntos. Podemos saber el número de líneas que habrá cuando juguemos con cualquier número de puntos (mayor que 4, porque debe haber 4 en las esquinas).
Otras respuestas
Varios participantes han hecho el siguiente razonamiento geométrico elegante y sencillo: en cualquier triangulación resultante al finalizar el juego, la suma de los ángulos de los triángulos entorno a un punto interior es 360º y en los cuatro puntos de las esquinas suman 90º. En total la suma de todos los ángulos de todos los triángulos es 7x360º + 4x90º = 2880º, que, dividido por 180º – lo que suman los ángulos de un triángulo cualquiera – , da el número de triángulos, 16, que tiene la triangulación. Teniendo en cuenta que cada triángulo tiene tres lados y cada línea de la triangulación, salvo las cuatro del borde del rectángulo, es compartida por dos triángulos, se obtiene que 3T+4 = 2L, siendo L el número de líneas y T el de triángulos. En consecuencia L es 26 y por eso gana siempre el jugador que comienza la partida.
Los lectores más matemáticos han empleado la conocida fórmula de Euler que relaciona el número de puntos con el de líneas y el de triángulos.
Cabe destacar que algunos participantes han empleado un método que, partiendo de cuatro puntos – situados en las esquinas del campo – los triangula con cinco líneas y añade los puntos interiores de uno en uno completando en cada paso una triangulación del terreno de juego. Observan que bastan tres líneas para completar la triangulación cada vez que se añade un punto interior. Así se obtienen 26 líneas cuando se han añadido todos los puntos. El método es correcto y demuestra que para cualquier posición de los puntos en las condiciones del problema hay una forma de terminar la partida con 26 líneas. Pero no queda probado que cualquier otra partida termine también con 26 líneas. Las reglas del juego no exigen que los jugadores sigan necesariamente ese esquema al trazar las líneas y hay de hecho triangulaciones que no se pueden obtener de esa forma.
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































