Más de 25.000 personas mueren cada año en Europa por la resistencia a los antibióticos
La UE denuncia que el suministro preventivo de antibióticos a animales y plantas aumenta la resistencia a estos fármacos en quienes consumen carne y verduras
La UE denuncia que el suministro preventivo de antibióticos a animales y plantas aumenta la resistencia a estos fármacos en quienes consumen carne y verduras
El argentino, que ha disputado los 90 minutos en 23 de los 24 partidos que acumula este curso, llegó exhausto a Barcelona tras el doble compromiso internacional con su selección, pero ya trabaja para jugar ante el Zaragoza
Jonathan Coe se sumerge en lo más profundo de las relaciones sociales con 'La espantosa intimidad de Maxwell Sim'
La imagen fue tomada en Marrakech en 1993 por el fotógrafo Albert Watson

Alfredo Pérez Rubalcaba viaja desde Huelva, Sevilla y Cádiz hasta Madrid Mariano Rajoy clausura un mitin en la capital onubense y vuelve a la capital
El agente, que estaba en la Academia de Baeza, se negó a jurar bandera

Mapa de la herencia que deja la última legislatura, empezando por lo más relevante: la crisis
El dispositivo y la descarga de libros, a partir del 23 de noviembre

Recordamos a las primeras ministras españolas que se atrevieron a posar en un editorial… y a otras cuantas más.
El representante del jugador considera que el defensa "ya ha hecho concesiones" y demanda ahora un esfuerzo del club
La patronal internacional del sector muestra su disposición a asumir la condonación, pero rechaza establecer un porcentaje. -La UE pactó que fuera del 50%
Juan José Cortés anuncia que el nuevo grupo religioso llevará su nombre

España está a punto de completar el cambio de Gobierno en los cuatro países del sur de Europa que hasta ahora más dificultades de financiación han sufrido
El organismo ha pasado a comprar la electricidad a precio variable en junio para optimizar costes
La socialista reivindica el subsidio agrario mientras la popular apuesta por aprovechar el crecimiento nacional
Una conductora perdió el control de su turismo al dar marcha atrás
La charla la impartía un profesor de la Universidad de Zaragoza en Salillas de Jalón en Zaragoza
Entreculturas presenta un informe sobre el acceso de las niñas a la escuela
Reuters revela que los dirigentes están negociando con el Fondo que el BCE le preste dinero para atajar la extensión de la crisis
Los jóvenes golpearon a las víctimas, de nacionalidad china y de 44 y 12 años, con un bate de béisbol
Los científicos señalan que puede haber "un cierto agotamiento del reservorio magmático"
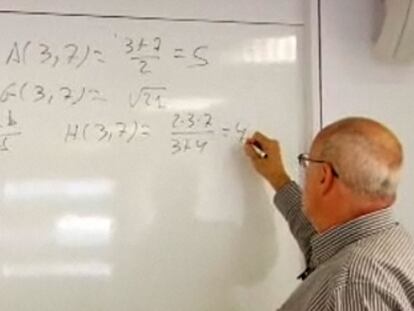

Desde Antonio Maura hasta Zapatero y Rajoy. Un siglo de looks electorales en España.
Primera jornada de huelga y de protesta a la que se enfrenta el Gobierno de los tecnócratas presidido por Monti
La septuagenaria directora brasileña presenta en España su filme 'Hotel Atlântico'

Los manifestantes critican “el Gobierno de los bancos” y las medidas de austeridad que plantea el nuevo Ejecutivo para salir de la crisis.- Dos heridos leves en los enfrentamientos en Milán

El desafío de esta semana, el 36º con el que celebramos el <a href="http://www.rsme.es/centenario/" target="blank">centenario de la Real Sociedad Matemática Española</a>, es el primero de los "desafíos de los lectores". Lo propuso, y lo presenta, <b>Pedro Carrión Rodríguez de Guzmán</b>, profesor en el <a href="http://www.murciaeduca.es/iesalcantara/sitio/" target="blank">IES Alcántara de Alcantarilla</a> (Murcia). Manda tu solución antes de las 00.00 horas del martes 22 de noviembre (medianoche del lunes hora peninsular española) al correo <a href="mailto:problemamatematicas@gmail.com">problemamatematicas@gmail.com</a>. Entre los acertantes sortearemos <a href="http://www.elpais.com/promociones/matematicas/">una biblioteca matemática</a> como la que cada domingo distribuye EL PAÍS en el quiosco. <p> Se han recibido un total de 150 propuestas de desafíos de los lectores, la inmensa mayoría muy adecuados para ser incluidos en la serie. La selección no ha sido sencilla, y la han realizado conjuntamente miembros de la RSME y de la redacción de elpais.com. Además de la calidad y la elegancia, se ha tomado en cuenta la variedad, tanto entre los 3 finalmente elegidos como con respecto a los restantes desafíos de la serie. Son sin duda criterios subjetivos, y muchos de los retos no seleccionados no desmerecen en nada a los que 3 que aparecerán y que se irán conociendo a medida que se graben.</p><p> Agradecemos mucho su interés a todos los participantes y esperamos que, aunque su propuesta no haya sido seleccionada, hayan disfrutado pensando posibles desafíos.</p><p> A continuación, <b>para aclarar las dudas y en atención a nuestros lectores sordos</b>, añadimos el enunciado por escrito del problema propuesto por Pedro Carrión.</p><p> La media aritmética de dos números se define como A(a,b)=(a+b)/2. Por ejemplo, A(3,7)=5</p><p> La media geométrica de dos números se define como G(a,b)=Raíz cuadrada de (axb). Por ejemplo, G(4,5)=Raíz (20)</p><p> Por último, la media armónica de dos números se define como H(a,b)=2/(1/a+1/b) que se puede simplificar operando algebraicamente como H(a,b)=2ab/(a+b). Por ejemplo, H(3,7)=2x3x7/ (3+7)= 4'2</p><p> El desafío de esta semana consiste en encontrar el menor primo p mayor que 100 para el que existe otro número entero distinto q, éste no necesariamente primo, de manera que las medias aritmética, geométrica y armónica de p y q sean números naturales.</p><p> Se considerarán correctas todas las soluciones que den valores válidos para p y q, pero, como siempre, nos gustaría que nos dijeseis cómo los habéis encontrado.</p><p> <a href="http://www.elpais.com/articulo/sociedad/desafios/matematicos/elpepusoc/20110712elpepusoc_8/Tes">DESAFÍOS ANTERIORES Y SUS SOLUCIONES</a> </p>