Un amigo del ministro de Economía italiano le paga los 8.500 euros del alquiler de su casa
La orden de detención por corrupción de Marco Milanese, su fiel asesor político, salpica a Giulio Tremonti
Detenidas 10 personas que ofrecían masajes en las playas de Roses
Interior tiene el objetivo de acabar con esta práctica ilegal
La izquierda reactiva
Y Alfredo P. vuelve a ser Rubalcaba
El candidato Rubalcaba tiene tirón y buena imagen en un sector muy amplio de la población
Sudán del Sur prepara su independencia
Sudán del Sur prepara su independencia
Aterrizaje de emergencia en Manises por un incendio en el motor
El avión, de las Fuerzas Armadas francesas, ha tomado tierra sin causar heridos
El móvil brasileño de Diego Costa
El delantero dice que se ha incorporado tarde al Atlético porque tenía otro número de teléfono
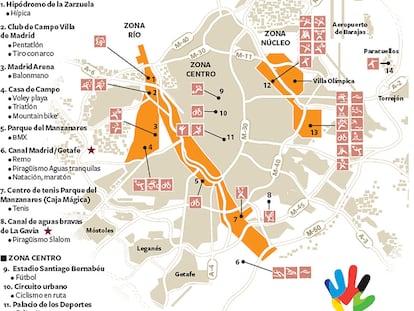
Así fue Madrid 2016
Una eliminatoria a brazo partido
Estados Unidos y España se enfrentan en cuartos de la Davis con tres de los diez mejores tenistas del mundo
Apátrida Messi
Que Leo meta goles parecidos a los de Diego no significa que sean jugadores parecidos...

Una mesa y un mantel
Alberto Castaño Domínguez, estudiante de doctorado en la <a href=" http://www.matematicas.us.es/index.php " target="blank">Facultad de Matemáticas de la Universidad de Sevilla</a>, presenta el decimoséptimo de los desafíos matemáticos con los que EL PAÍS celebra el <a href="http://www.rsme.es/centenario/" target="blank">centenario de la Real Sociedad Matemática Española</a>. Envía tu solución antes de las 00.00 horas del martes 12 de julio (medianoche del lunes) a la dirección <a href="mailto:problemamatematicas@gmail.com">problemamatematicas@gmail.com</a> y gana <a href="http://www.elpais.com/promociones/matematicas/">una biblioteca matemática</a> como la que cada semana distribuye EL PAÍS. Esta semana en el quiosco, por 9,95 euros con el periódico, <i>Al otro lado del espejo</i>, por Joaquín Navarro.<p> A continuación, para aclarar dudas y en atención a nuestros lectores sordos incluimos el enunciado del problema por escrito.</p><p> Esta semana partimos del supuesto de que tenemos una mesa de 90 cm de ancho por 1,5 m de largo y queremos cubrirla con un rollo de papel que hemos comprado. El rollo tiene exactamente 20 cm de ancho, sólo podemos hacer cortes transversales y su área es idéntica a la de la mesa, por lo que no podremos desperdiciar ningún trozo ni superponerlo a otro. Además, al poner los trozos de mantel, solo se podrá hacer en horizontal o en vertical, nunca en diagonal. El desafío es encontrar una manera de cubrir la mesa o, si no se puede hacer, demostrar por qué.</p><p> <b>Nota importante</b>: Han llegado ya varias soluciones erróneas porque no tienen en cuenta que el papel hay que cortarlo <b>transversalmente</b>, no longitudinalmente o de forma diagonal. Es decir, las tiras de papel deben mantener el ancho de 20 centímetros.</p><p><a href="http://www.elpais.com/articulo/sociedad/estrella/ojos/elpepudep/20110705elpepusoc_5/Tes">VER LOS 16 PROBLEMAS ANTERIORES</a> </p>
"En algún momento no veía nada"
"Lo importante era salvar el día y no caerse", dice Contador
Viola a una joven y luego va con su hermano a matar al padre
La policía detiene a dos hombres como presuntos autores de las agresiones
La matrícula de las universidades se encarece un 5%, y la de los másteres, un 30%
González defiende tras el Consejo de Gobierno que tras la aprobación de la medida "no llega a cubrirse ni el 14% del coste real de enseñanza de cada alumno universitario "
Los DVD de la semana
Un drama sobre el boxeador irlandés Micky Ward y un thriller español protagonizado por Mario Casas, ya a la venta
Molt 'soroll' per a poca cosa

Un nuevo Rubalcaba humanizado
El consultor político Antoni Gutiérrez-Rubí evalúa la imagen y el lema del candidato socialista

Los micrófonos abiertos, eternos enemigos de los políticos
Las líneas abiertas provocan las escuchas más divertidas de los líderes políticos
Del periodismo amarillo al periodismo basura
L' 'APM' i l'espectacle 'friqui'
Machu Picchu, 100 años después
Machu Picchu, 100 años después
El presidente yemení reaparece desde Arabia Saudí
La televisión yemení emite una alocución de Ali Abdulá Saleh, en la que se abre al diálogo, pero no habla de retorno
Dretes i esquerres
Un Mundial de cara a los Juegos
La Federación Española de Natación presenta en Barcelona la delegación que acudirá al torneo de Shanghái
La sindicatura de Cuentas de Cataluña acumula en caja 22,8 millones
El organismo de control contable de la Generalitat entregó hace un mes al consejero de Economía 3,1 millones sobrantes de 2009
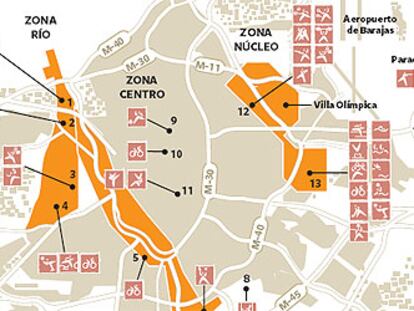
El Gobierno regional advierte del "enorme esfuerzo" de intentar un Madrid 2020
Gallardón abre una ronda de consultas para decidir si Madrid lo intenta por tercera vez.- Lissavetzky dice que requeriría explicar a la sociedad "cuánto costaría" y cómo se pagaría