Lo que sabemos de las superficies a través de sus puntos singulares

Más información

El dominó binario de Gardner

Dominar el dominó

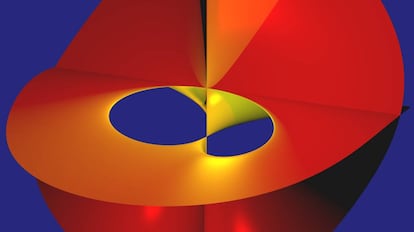
Es Miau. No es un gato, y tampoco un sacacorchos. Es una figura matemática; en concreto, es la superficie representada por la fórmula 𝑥²𝑦𝑧+𝑥²𝑧²+2𝑦³𝑧+3𝑦³=0. Tres letras (estas misteriosas x, y, z del final del alfabeto), algunos números y una igualdad. La expresión evoca interminables clases en la escuela, cuando nos abandonaban a estos símbolos y enigmas que nos traían de cabeza. Pero más allá de nuestros recuerdos nostálgicos, esta combinación de letras y números contiene, de un modo aún desconocido para el lego, toda la información sobre la geometría, la curvatura, la ubicación de las puntas y de los ejes de la figura. El campo de las matemáticas que explica esta relación entre ecuaciones y figuras se llama geometría algebraica. Es un campo clásico, difícil y muy popular en la investigación actual. Hay todo un diccionario que hace equivaler las propiedades geométricas de las superficies con las propiedades algebraicas de las ecuaciones correspondientes. Se pueden calcular curvaturas, puntos de intersección, puntas, áreas, agujeros, pliegues, y muchas cosas más. Estos objetos matemáticos configuran todo un zoo, y sobre ellos hay una teoría enormemente estética y satisfactoria.

Pero lo cierto es que, por muy bonita que sea, a primera vista, poco podemos entender de la ecuación anterior. Tratemos de explorarla desde el punto de vista geométrico. Quizás merece la pena dar la vuelta al dibujo, verlo desde detrás.Parece ser que se esconde una rana que croa:

Ahora vemos un agujero (¿o dos?), dos puntas que casi se tocan, una recta horizontal, y una amplia bóveda, con luz y color de reverberación. La figura parece ser simétrica: la parte de izquierda es idéntica a la parte derecha, ¿o no?. Desde otras perspectivas, podemos ver las figuras de abajo. Aparecen ejes de intersección, hojas, curvaturas, cambios de orientación. Lo cierto es que seguimos sin entender demasiado.

Dos de sus ejes son visibles en la superficie (como puede verse en las imágenes 3, 4 y 5), y en ellos “ocurren” singularidades. Estos son puntos donde la geometría se distingue sustancialmente del resto (que se llaman puntos lisos o regulares). Son puntos muy particulares, casi extraordinarios: o bien intersecciones de hojas (horizontalmente a lo largo del eje x), o bien aristas (verticalmente a lo largo del eje z), o bien puntos aún más especiales como el espigón en el punto de intersección de los tres ejes.

En los puntos lisos de una variedad la vida es un poco aburrida: es como un llano, o una colina muy suave. En un punto singular hay sorpresas, vértigos y rincones escondidos: la geometría local es mucho más rica, y su comprensión permite entender ciertos fenómenos “catastróficos”. En ciencias naturales estos puntos se corresponden a cáusticas en óptica, singularidades en física y teoría de ondas, es decir, remolinos, agujeros negros, la ruptura de una ola… son aquellos sucesos en los que, de repente, se perturba la calma y aparece un desgarro. Entender cómo se forman y cómo evolucionan es clave para describir estos fenómenos.

Es por ello que los matemáticos dedican una gran cantidad de esfuerzos a responder preguntas del tipo: ¿cómo se forman las singularidades? ¿Cómo se detectan en la ecuación? Existen cuestiones infinitas sobre las singularidades, algunas están resueltas y otras siguen siendo misterios para los matemáticos que las estudian. Uno de los resultados conocidos más importantes es el teorema de resolución de singularidades de variedades algebraicas (una generalización del concepto de superficie) en característica zero, probado por el matemático japonés Heisuke Hironaka, medalla Fields en 1970. Dice que cualquier singularidad es la sombra de una superficie lisa sin singularidades, y así permite entender matemáticamente cómo nacen las singularidades. Es un resultado profundo, muy difícil de demostrar y con muchísimas aplicaciones, que nos permitirán en el futuro comprender mejor la naturaleza de algunas catástrofes.

Además, abre preguntas aún por responder, como la llamada resolución en característica positiva, una extensión del resultado de Hironaka a variedades de característica mayor que cero.Este resultado reta a grandes matemáticos desde hace más de cincuenta años. Por el momento, no se sabe si es cierta o falsa, y los científicos tienen que vivir con esta incertidumbre, este vértigo, hasta que una de las dos opciones se haya verificado.

Herwig Hauser es profesor de la Universidad de Viena (Austria) y creador de las imágenes de superficies algebraicas clásicas IMAGINARY que ilustran este artículo.

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.