Un cuerno finito-infinito

El mundo de las matemáticas está repleto de figuras con características interesantes o con propiedades curiosas. En ocasiones, estas figuras tienen una definición extraña o son creadas expresamente para que posean esas propiedades que resultan sorprendentes o que, de alguna manera, atentan contra nuestra intuición.

No es el caso de la figura que nos ocupa hoy. Su definición es relativamente sencilla y, sin embargo, presenta una curiosa característica que relaciona lo finito y lo infinito. Nos referimos al conocido como cuerno de Gabriel.

El cuerno de Gabriel (también llamado trompeta de Torricelli), se puede construir de la siguiente forma: tomamos la porción de la curva f(x)=1/x, desde el punto x=1 hasta infinito, y la giramos en torno al eje X. Con esto obtenemos una superficie tridimensional, que es la que se conoce como cuerno de Gabriel. En la imagen podéis ver la representación de la curva y la figura tridimensional que quedar al girar en torno al eje X.

Imaginemos ahora que queremos pintar la superficie externa del cuerno de Gabriel. Sí, pintar, con pintura y brocha. Teniendo en cuenta que la superficie es infinita, no sería descabellado pensar que necesitaríamos pintura infinita para poder conseguir nuestro objetivo. Pues sí, es correcto: necesitaríamos infinita pintura para poder pintar la superficie externa del cuerno de Gabriel.

Supongamos ahora que lo que queremos hacer es rellenar el interior del cuerno con pintura. Como antes, no sería ninguna locura pensar que volveríamos a necesitar pintura infinita para ello, pero en este caso no es así: podríamos rellenar el interior del cuerno de Gabriel con una cantidad finita de pintura.

El tema de la pintura es un intento de acercar a la realidad una cuestión que es meramente matemática. En realidad, lo que estamos haciendo es considerar pintura, digamos, “ideal”, y la cuestión de pintar la superficie del cuerno tendría que ver con el área del mismo, al igual que rellenarlo está relacionado con su volumen. En definitiva, la cuestión es que el cuerno de Gabriel es una superficie tridimensional con área infinita y volumen finito. Y ésa es la característica más curiosa y, en cierto modo, contraria a la intuición que podríamos tener al pensar en ello.

El cálculo de los valores del área y el volumen de esta interesante figura se puede hacer de manera relativamente sencilla mediante integrales, aunque en este caso, por tener un rango de 1 a infinito, necesitaremos integrales impropias. Para calcular el volumen, tendremos que integrar el cuadrado de la función que genera nuestro cuerpo de revolución y multiplicar el resultado por Pi. Y para el área, integramos el producto de la función por la raíz cuadrada de 1 más la derivada de la función al cuadrado, y después multiplicamos el resultado por 2Pi.

En nuestro caso, como tenemos que usar integrales impropias, tendremos que tomar límites después de calcular las integrales. También es interesante destacar que para calcular el área hemos acotado inferiormente la integral correspondiente por otra que se calcula más fácilmente. Aquí tenéis los desarrollos de cada uno de estos cálculos:

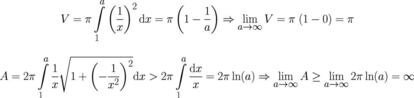
Por cierto, es interesante resaltar que la situación contraria a la que se da en esta superficie no se puede presentar. Es decir, no podemos tener una superficie de este tipo que tenga superficie finita y volumen infinito.

El hecho de que el volumen del cuerno de Gabriel sea finito fue descubierto por el matemático italiano Evangelista Torricelli a mediados del siglo XVII, y en su momento se consideró como una paradoja, generando cierta controversia entre los matemáticos y pensadores de la época. Teniendo en cuenta que en ese momento histórico todavía no se había desarrollado el cálculo (es decir, no “había” integrales), ¿cómo pudo hacerlo? Pues con su método de los indivisibles, una extensión del conocido como principio de Cavalieri. En este enlace tenéis información sobre la demostración de Torricelli.

Espero que, a quienes no lo conocíais, os haya resultado interesante la presentación del cuerno de Gabriel. Y también espero que los que ya lo conocíais hayáis desfrutado recordando de nuevo las interesantes características de esta figura. Sea cual sea el grupo al que pertenezcáis, es posible que esta superficie os haya traído a la mente más objetos matemáticos que consideréis procedente mencionar. Si es así, os agradecería que lo hicierais en los comentarios.