Culebrón matemático

EL PAÍS y Materia proponen a sus lectores, cada semana, un juego de lógica. Los lectores pueden enviar sus soluciones en los comentarios, y plantear nuevos acertijos y juegos. La respuesta correcta será ofrecida en la columna de la semana siguiente.

“En el Gran Templo de Benarés, bajo la cúpula que señala el centro del mundo, hay una placa de latón con tres agujas de diamante, cada una de las cuales tiene una altura de un codo y es tan gruesa como el cuerpo de una abeja. El día de la creación, Brahma ensartó en una de esas agujas 64 discos de oro de diferentes diámetros: el disco más grande apoyado en la placa, y luego, uno encima de otro, los 63 restantes, en orden decreciente. Día y noche, el sacerdote de turno transfiere los discos de una aguja a otra, de acuerdo con las leyes de Brahma, fijas e inmutables, que requieren que el sacerdote mueva solo un disco a la vez, y que los coloque en las agujas de forma que nunca haya un disco encima de otro de menor tamaño. Cuando termine el traslado de todos los discos de la aguja inicial a una de las otras dos, el templo se convertirá en polvo y el universo entero desaparecerá”.

No es un fragmento de los Vedas, sino el folleto de un juguete, un rompecabezas inventado en el siglo XIX por el matemático francés Édouard Lucas y comercializado como “La torre de Hanói” (con solo cinco discos de madera en lugar de los 64 discos de oro de Brahma).

Casualmente, y como vimos la semana anterior, por la misma época William Hamilton también difundió uno de sus descubrimientos en forma de rompecabezas. Una de las versiones era un dodecaedro de madera con el nombre de una ciudad escrito junto a cada vértice; el juego consistía en partir de un vértice cualquiera y, siguiendo las aristas, recorrer todas las ciudades pasando una sola vez por cada una de ellas y regresando al punto de partida. En la figura vemos una de las soluciones posibles.

Dos grandes matemáticos del siglo XIX coinciden, cosa ya de por sí extraordinaria, en comercializar como juguetes sus respectivos descubrimientos topológicos. Y, como en los culebrones, esos dos tránsfugas de la ciencia que sin conocerse de nada coinciden en una juguetería resultan ser hermanos, aunque no lo descubrirían hasta cien años después. A mediados del siglo pasado, el matemático estadounidense D. W. Crowe demostró que el orden en el que hay que mover n discos de una torre de Hanói para trasladarlos a otro eje, se corresponde exactamente con la secuencia direccional (y dimensional) de un recorrido hamiltoniano en un cubo de n dimensiones.

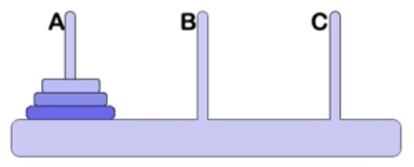
Traslada los tres discos del eje A al B o al C en el menor número de movimientos posible (de acuerdo, claro está, con las fijas e inmutables leyes de Brahma), y luego comprueba el isomorfismo de esta transferencia de discos con un recorrido hamiltoniano en un cubo normal y corriente (o sea, de tres dimensiones).

Y aunque no tengas tiempo de trasladar los 64 discos de oro (ni lo intentes, no vaya a ser que desaparezca el universo), tal vez descubras la sorprendente relación de esta mítica transferencia con la recompensa que el no menos mítico inventor del ajedrez le pidió al rey de la India: un grano de trigo por la primera casilla del tablero, dos por la segunda, cuatro por la tercera, ocho por la cuarta, y así sucesivamente hasta la casilla 64, doblando en cada una el número de granos de trigo de la anterior.

Carlo Frabetti

Escritor y matemático, miembro de la Academia de Ciencias de Nueva York, ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’