La paradoja de las ánforas
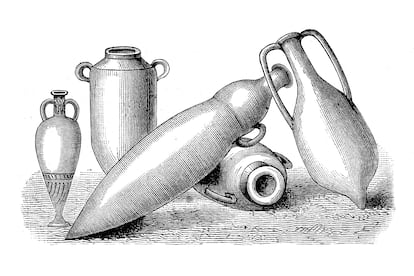
¿Por qué las ánforas romanas tenían una forma puntiaguda que no permitía que quedaran en equilibrio sobre su base?

La semana pasada vimos una solución al problema de unir una cuadrícula de 4x4 puntos con solo seis trazos rectilíneos sin levantar el lápiz del papel ni pasar dos veces por un mismo trazo. He aquí otra, elegantemente simétrica y cíclica:
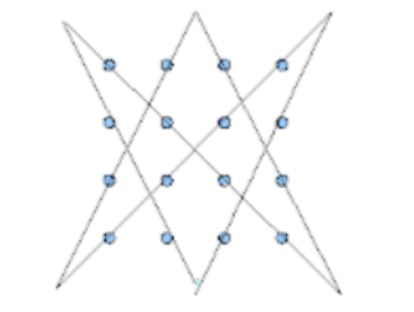
En el caso de la cuadrícula de 3x3, la solución es única, pero no sé cuántas soluciones distintas hay para la de 4x4 (por lo menos tres, pero tal vez haya más), y es de suponer que a medida que aumenta el número de puntos, aumentará también el número de soluciones distintas.
En cuanto a las tapas de las alcantarillas, hay al menos tres razones de peso (nunca mejor dicho) para que sea preferible (aunque no imprescindible) que sean redondas. Al ser circulares, se pueden trasladar haciéndolas rodar, lo cual es muy conveniente teniendo en cuenta su considerable peso. Además, ajustan en su hueco en cualquier posición, mientras que si fueran cuadradas o de otras formas habría que girarlas hasta hacerlas coincidir exactamente con el hueco. Y, no menos importante, al ser redondas no pueden caer por su propio hueco, cosa que sería relativamente fácil si fueran cuadradas, ya que la diagonal de un cuadrado es casi vez y media su lado. Lo cual da pie a plantear la siguiente pregunta: ¿Hay otra posible forma de tapa de alcantarilla que no permita que se caiga por su propio hueco, o solo la tapa circular tiene esta propiedad?
¿Y por qué podemos tener la certeza de que las hojas de los sables son arcos de circunferencia? Al menos en el caso de los que tienen vaina, como las katanas, ha de ser forzosamente así, pues la recta y la circunferencia son las únicas líneas que pueden deslizarse sobre sí mismas (bueno, en realidad hay una tercera, ¿cuál es?). Si la curvatura de los sables no fuera un arco de circunferencia, no podrían introducirse en sus vainas.
La poderosa razón de la abundancia de triángulos en estructuras de todo tipo es que se trata del único polígono que queda determinado por la longitud de sus lados. Si nos dicen que los lados de un cuadrilátero miden todos ellos 10 cm, puede ser un cuadrado o un rombo (mejor dicho, infinidad de ellos), mientras que si nos dicen que los lados de un triángulo miden 10, 20 y 30 cm, sabemos que solo puede ser un triángulo rectángulo. Y pasando de la geometría a la física, eso significa que un triángulo es indeformable (a no ser que lo rompamos), mientras que, por ejemplo, un cuadrado de vértices articulados se deforma fácilmente. Por consiguiente, las estructuras de módulos o celdas triangulares son más resistentes que las basadas en cuadrados, rectángulos u otros polígonos.
Y hablando de cuadrados y rectángulos, hay distintas razones para su sobreabundancia en todo tipo de obras y productos humanos (no así en la naturaleza). Por una parte, la atracción gravitatoria nos impone el binomio horizontal-vertical: nuestro peso -vertical- hace conveniente que nos movamos preferentemente sobre superficies horizontales para mayor estabilidad (por eso dice Le Corbusier que el ángulo recto es nuestro pacto de solidaridad con la naturaleza). Pero, por otra parte, los objetos ortoédricos (cajas, ladrillos, baldosas…) se apilan y ensamblan más fácilmente y con mayor aprovechamiento del espacio. En el caso de ladrillos y tatamis, el hecho de que un lado del rectángulo sea el doble que el otro facilita la construcción de estructuras compactas y estables.
Sin embargo las ánforas de los antiguos romanos, magistrales ingenieros y eficientes diseñadores industriales avant la lettre, eran vasijas puntiagudas, que no podían sostenerse sobre su propia base y tenían una relación superficie-volumen poco ventajosa. ¿Por qué?
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































