El trabajo que cambió la dinámica de los fluidos cumple 100 años

En 1923 se publicó Stability of a viscous liquid contained between two rotating cylinders, un texto revolucionario firmado por el matemático y físico Geoffrey Ingram Taylor (1886, Londres- 1975, Cambridge). La investigación plasmada en él abrió nuevas vías para entender los patrones que aparecen en un flujo, como los que se observan en el movimiento del océano. Un siglo después, el trabajo continúa proporcionando una base sólida para una amplia gama de estudios científicos y aplicaciones prácticas. Por ejemplo, es clave para comprender cómo se desarrolla la turbulencia a partir de un flujo estable, es decir, cómo se pasa de un flujo ordenado a otro caótico y en continuo cambio.

El artículo supone el comienzo de la llamada teoría de la estabilidad hidrodinámica. Esta rama de la física y las matemáticas trata de entender las inestabilidades en un fluido, pequeñas perturbaciones que hacen que el flujo se desvíe de su estado inicial y evolucione hacia una configuración diferente. Se forman, por ejemplo, al friccionar un fluido en movimiento y una superficie sólida y pueden amplificarse con el tiempo y provocar cambios notables en el flujo, como la aparición de vórtices o remolinos.

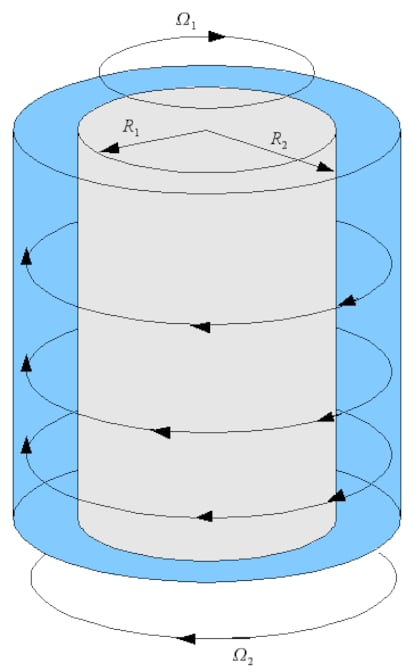
Durante siglos, físicos y matemáticos trataron de encontrar un criterio para detectar el momento en el que aparecen las inestabilidades, a partir de las propiedades del fluido y las ecuaciones y parámetros que describen su movimiento. La teoría de Lord Rayleigh supuso un primer paso para resolver esta cuestión: ofreció un modelo teórico para predecir la estabilidad de un fluido sin viscosidad —es decir, que no presenta resistencia a fluir—. En particular, demostró que el flujo es estable siempre que se satisfaga cierta condición —el cuadrado del momento angular por unidad de masa del fluido aumenta hacia afuera—. Esto significa que, si solo gira el cilindro interior, el flujo es inestable, mientras que, si gira únicamente cilindro exterior, es estable.

En 1890, el físico Maurice Couette publicó su tesis doctoral sobre la fricción entre un fluido en movimiento y una superficie sólida. Para poder medir la viscosidad, diseñó un dispositivo experimental formado por dos cilindros concéntricos —uno interior, fijo, y otro exterior, giratorio— con líquido entre medio. Al rotar el cilindro exterior, se generaba un flujo en el fluido y podía cuantificar la fricción producida, es decir, su viscosidad. Su aporte fue tan importante que, pronto, el nombre de Couette se asoció a los flujos que estudió. Casi al mismo tiempo, y de forma independiente, Arnulph Mallock, maestro en construir experimentos, describió la inestabilidad centrífuga que ocurre cuando el cilindro interior rota y el exterior permanece quieto.

El siguiente paso era unir estas observaciones experimentales con la formalización matemática de Rayleigh. Fue precisamente lo que hizo Geoffrey Ingram Taylor, que se dio cuenta de que, en el caso de fluidos no viscosos, los experimentos coincidían con la teoría. Taylor, nieto del célebre matemático George Boole, escribió: “Parece dudoso que podamos comprender completamente la inestabilidad del flujo de un fluido sin obtener una representación matemática del movimiento de un fluido en algún caso particular en el que se pueda observar la estabilidad real”. Por tanto, para empezar a entender —con las herramientas matemáticas de Rayleigh— las inestabilidades del flujo de Couette, era esencial encontrar un buen ejemplo que analizar.

Taylor consideró que no solo uno, sino que los dos cilindros concéntricos rotan. Construyó el dispositivo y con él, y el uso de herramientas matemáticas, predijo la estabilidad del fluido. Para ello, linealizó las ecuaciones de Navier-Stokes —que describen el comportamiento de un fluido—. Es decir, asumió que las perturbaciones eran lo suficientemente pequeñas como para despreciar parte de los términos en la ecuación, y encontró soluciones de las ecuaciones que se corresponden con las inestabilidades observadas en los experimentos.

Las ecuaciones permiten también determinar si crece la inestabilidad —es decir, si el flujo inestable puede dar lugar a formas más complejas— o disminuye con el tiempo —es decir, si el flujo quedará estable, sin cambios—. Así, Taylor logró describir teóricamente el comportamiento del fluido, en función de sus propiedades y de las velocidades de rotación de los dos cilindros.

En 1923 publicó en Philosophical Transactions of the Royal Society A su trabajo. La estrecha concordancia entre sus resultados teóricos y experimentales no tenía precedentes en la historia de la mecánica de fluidos, por lo que el documento se describe como la primera prueba convincente de la aplicabilidad de los enfoques matemáticos para predecir la estabilidad de un fluido.

Su trabajo conectó las matemáticas, la física y la ingeniería y, en los siguientes años, fue utilizado en numerosos estudios relacionados con la estabilidad, los flujos astrofísicos y geofísicos, la dinámica no lineal o los aspectos fundamentales de la turbulencia. Desde entonces, este flujo —llamado de Taylor—Couette— ha sido ampliamente estudiado y ha brindado una valiosa plataforma para explorar y comprender los principios básicos que rigen el comportamiento de los fluidos en rotación.

Prueba de ello es la reunión bianual que se celebra desde hace más de 40 años, donde se junta una comunidad internacional creciente interesada en los diversos patrones de flujo observados en el aparato de Taylor—Couette. El pasado verano, el encuentro tuvo lugar en Barcelona, donde el 100 aniversario de la publicación de Taylor fue la excusa para seguir hablando de inestabilidades, vórtices y fascinantes patrones geométricos.

Jezabel Curbelo es investigadora Ramón y Cajal del Departamento de Matemáticas de la Universitat Politècnica de Catalunya (UPC) y miembro del Instituto de Matemáticas de la UPC (IMTech) y del Centre de Recerca Matemàtica (CRM).

Ágata Timón García—Longoria es coordinadora de la Unidad de Cultura Matemática del Instituto de Ciencias Matemáticas (ICMAT).

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.